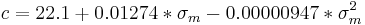Odermattekvationen
Från Rilpedia
Odermattekvationen är en semiempirisk ekvation som beskriver pilars penetration i monolitiskt pansar. Den används för att uppskatta penetrationsförmågan hos moderna pilprojektiler.
D penetratorns diameter [mm]
L total längd av penetrator [mm]
Lw arbetande längd av penetrator [mm]
vT anslagshastighet [m/s]
α anslagsvinkel [°] 0° är vinkelrätt mot målet
ρP penetratorns densitet [kg/m3]
ρT målets densitet [kg/m3]
σm målets brottgräns [MPa]
P penetrationskanalens längd [mm]
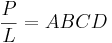
Innehåll |
A beskriver inverkan av pilens slankhet
Denna term går mot 1 för långa pilar
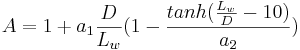
a1 = 3.94 och a2 = 11.2 gäller för 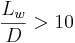
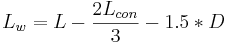
B beskriver inverkan av anslagsvinkeln
B = cos(α)m
Där m = − 0.225
C beskriver inverkan av målet och penetratorns densiteter
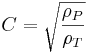
D beskriver inverkan av hastighet och materialegenskaper
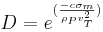
Där