Neurala nätverk

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Ett artificiellt neuralt nätverk består av flera sammankopplade noder, eventuellt i flera lager.

Neurala nätverk är ett samlingsnamn på ett antal algoritmer för informationsbehandling som försöker efterlikna funktionen i nervceller och hjärnor. Neurala nätverk kan också betyda de nätverk som förekommer i naturen, men oftast är det den artificiella varianten som avses. Om man önskar vara specifik kan man säga artificiella neuronnät - ANN.

Algoritmer som bygger på neurala nätverk kan ofta klara problem som är svåra att lösa med konventionella datalogiska metoder. Exempel på tillämpningar är: mönsterigenkänning, signalbearbetning, reglerteknik, prognoser, självorganisering, problem med många bivillkor, schemaläggning.

Precis som den mänskliga hjärnan måste neurala nätverk tränas innan de kan användas. De flesta neurala nätverk arbetar därför i två faser, först en inlärningsfas där nätet tränas på den uppgift som ska utföras, sedan följer en tillämpningsfas där nätet bara använder det som det har lärt sig. Naturligtvis går det att låta nätet fortsätta lära sig även när det används, men vanligen lämnas det som det är när det uppnått den precision som eftersträvades för tillämpningen.

Innehåll

1 Uppbyggnad
- 1.1 Grundelement
  - 1.1.1 Kärnan
    - 1.1.1.1 Summation
    - 1.1.1.2 Transferfunktion
- 1.2 Nätverk
  - 1.2.1 Övervakade nätverk
  - 1.2.2 Oövervakade nätverk
2 Tillämpningar
- 2.1 Exempel på neurala nätverk samt användningsområde
3 Typer av neurala nätverk
4 Extern litteratur

Uppbyggnad

Grundelement

Alla neurala nätverk har en grundbyggsten: neuronen (kallas också omväxlande nod, cell, enhet). I konstgjorda neurala nätverk abstraherar man neuronen till att bestå av en eller flera ingångar (dendriter), en kärna (soma) samt en utgång (axon).

På varje ingång, v_j⁽ⁱ⁾, sitter det en vikt w_j⁽ⁱ⁾. Grundidén är att en mängd neuroner sitter ihoplänkade i olika strukturer och vikterna ändras för att uppnå olika resultat. Neurala nätverk måste tränas upp till önskad funktion.

Kärnan

Kärnan består av två separata delar, summationsdelen och transferfunktionen. Det finns även en specialingång v₀ med vikten w₀ som möjliggör justering av alla ingångsvärden (bias). Ingångarna är anslutna till summationsdelen och utgången (Y⁽ⁱ⁾) är ansluten till transferfunktionen.

Summation

Summationsdelen summerar ihop alla ingångar och väger ihop vikterna enligt:

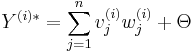
$Y^{(i)*} = \sum_{j=1}^n v_j^{(i)}w_j^{(i)} + \Theta$

Där $Θ$ är bias-ingången: 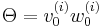$\Theta = v_0^{(i)}w_0^{(i)}$

Transferfunktion

Transferfunktionen består av: 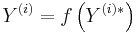$Y^{(i)} = f\left( Y^{(i)*} \right)$

Där transferfunktionen kan ha flera olika utseenden: tröskelfunktion, linjärfunktion, sigmoidfunktion, tangens hyperbolicus med flera.

Nätverk

Ett konstgjort neuralt nätverk består av godtycklig mängd neuroner. Nackdelen med neurala nätverk är att de måste tränas till önskad funktion. Det betyder att nätverket först måste matas med kända mätdata och utdata innan nätverket kan tas i bruk. Neurala nätverk delas in i två huvudgrupper: övervakade och oövervakade.

Övervakade nätverk

Övervakade nätverk tränas upp genom att mata det med kända mätdata och kända svar. Om resultatet skiljer sig från det kända svaret beräknas hur stort felet är och vikterna på ingångarna i varje neuron justeras. Detta förfarande itereras och om nätet är rätt designat (där faktorer såsom val av nätverk, antal neuroner, val av träningsdata spelar en avgörande roll) så konvergerar nätet mot ett "korrekt" beteende.

Oövervakade nätverk

Oövervakade nätverk är ett självlärande system som används till att hitta kända och okända relationer mellan data. Nätverket matas med data men operatören av nätverket tillåts inte justera vikterna efter vad som kommer ut. Efter ett tag (om det finns relationer mellan ingångsdata samt att antalet neuroner är tillräckligt) konvergerar nätet.

Tillämpningar

Neurala nät har en mängd användningsområden, och nya användningsområden skapas hela tiden. Exempel på sådana är:

Mönsterigenkänning
Signalbearbetning
Reglerteknik
Prognoser (till exempel: väderlek, börskurser(se Teknisk analys)
Självorganisering
Lösning av problem med många/svåra villkor (till exempel schemaläggning, handelsresandeproblemet)

Exempel på neurala nätverk samt användningsområde

Problem	Nätverk	Beskrivning	Typ av träning
Klassifikation	Learning Vector Quantization, LVQ; Counterpropagation; Självorganiserande kartor, SOM	För att dela in data i bestämda klasser	Kombination av övervakad och oövervakad träning
Prognosframställning	Backpropagation	Att kunna ge prognoser om framtida händelser med hjälp av ingångsdata	övervakad
Visualisering	Självorganiserande kartor, SOM; Adaptive Resonance Theroy, ART	Att åskådliggöra okända korrelationer mellan ingångsdata	oövervakad
Association	Hopfieldnät, Hammingnät	Att lära sig mönster och att kunna återskapa störda varianter av dessa	övervakad

Typer av neurala nätverk

Perceptronen

Ett viktigt och mycket enkelt neuralt nätverk är den så kallade perceptronen. Den beskrevs redan på 1950-talet av

För att perceptronen skall fungera måste datan vara linjärt separerbar.

Det upptäcktes tidigt att perceptronen har begränsad kapacitet att lösa problem. Ett exempel på ett problem som inte kan lösas är XOR.

$\delta w = \nabla x$

Flerlagersperceptroner

ART

Adaptive resonance theory. Bygger på att ett mönster måste resonera med ett tidigare mönster för att läras inj

Neokognitron

Extern litteratur

Wikimedia Commons har media som rör Neurala nätverk
Bilder & media

Samling av studier om aktieprediktion med neurala nätverk
T. Kohonen: Self-Organizing Maps, Springer, 1995
U. Seiffert & L.C Jain: Self-Organizing Neural Networks, Springer, 2001
W. Maass & C.M Bishop: Pulsed Neural Networks, MIT Press, 1999