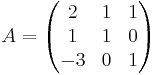Matrisers teckenkaraktär
Från Rilpedia
Inom matematiken anger teckenkaraktären hos en matris A vilka tecken v * Av (v * är det hermiteska konjugatet till v) antar för alla vektorer v.
Om A är en 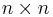 matris och
matris och 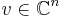 säger man att A är:
säger man att A är:
- Positivt definit om
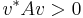 för alla
för alla 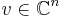 .
.
- Positivt semidefinit om
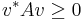 för alla
för alla 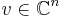 .
.
- Negativt definit om
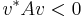 för alla
för alla 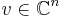 .
.
- Negativt semidefinit om
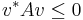 för alla
för alla 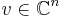 .
.
- Indefinit om A varken är positivt eller negativt semidefinit
Att avgöra teckenkaraktär
Det finns flera sätt att avgöra en matris teckenkaraktär.
Egenvärden
Om A är en diagonaliserbar matris och alla egenvärden är positiva är A positivt definit. Om alla egenvärden är negativa är matrisen negativt definit. Om minst ett egenvärde är noll, men de nollskilda egenvärdena har samma tecken är matrisen semidefinit. Om egenvärdena har olika tecken är matrisen indefinit.
Sylvesters kriterium
Enligt Sylvesters kriterium är en matris A positivt definit om och endast om varje determinant till delmatriserna uppifrån till vänster (inkluderat matrisen själv) är positiva.
Exempelvis kan man avgöra om matrisen nedan är positivt definit:
För att avgöra detta betraktar vi de övre vänstra delmatriserna:
- detA1 = | 2 | = 2
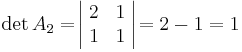
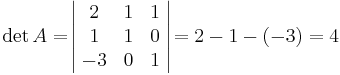
detA1,detA2detA > 0 och alltså är A positivt definit.