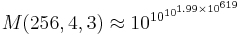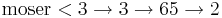Steinhaus-Mosers notation

Från Rilpedia

(Omdirigerad från Mosers tal)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Steinhaus–Mosers notation är ett sätt inom matematiken att uttrycka extremt stora tal. Notationen är uppkallad efter Hugo Steinhaus och Leo Moser. Det är en utökning av Steinhaus polygonnotation (se nedan).

, talet n i en triangel, betyder nⁿ, det vill säga n upphöjt till n.

, talet n i en kvadrat, betyder "talet n inuti n stycken trianglar".

, talet n i en femhörning, betyder "talet n inuti n stycken kvadrater".

Detta går att generalisera till godtycklig månghörning, så att n skrivet i en (m+1)-hörning är ekvivalent med "talet n inuti n stycken m-hörningar".

Exempel, talet 2 i en kvadrat är det samma som talet 2 i två trianglar, det vill säga

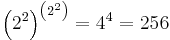$\left(2^2\right)^{\left(2^2\right)} = 4^4 = 256$ .

Steinhaus polygonnotation

I Steinhaus polygonnotation är endast triangeln, kvadraten och en cirkel, , definierade. Cirkeln är ekvivalent med femhörningen ovan.

Steinhaus definierade:

"mega" är talet 2 i en cirkel:
"megiston" är talet 10 i en cirkel:

Mosers tal är talet "2 i en megagon", där en "megagon" är en "megahörning", dvs en månghörning med "mega" stycken sidor.

Alternativa notationer

Använd funktionerna square(x) och triangle(x)
låt M(n,m,p) vara talet som representeras av talet n i en m-nästlad p-hörning; sedan följer:
- $M (n,1,3) = n n$
- $M (n,1, p + 1) = M (n, n, p)$
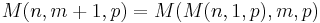
- $M(n,m+1,p) = M\big(M(n,1,p),m,p\big)$

och

- mega = $M (2,1,5)$
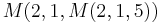
- moser = $M\big(2,1,M(2,1,5)\big)$

Mega

Notera att är redan det ett mycket stort tal, eftersom = square(square(2)) = square(triangle(triangle(2))) = square(triangle(2²)) = square(triangle(4)) = square(4⁴) = square(256) = triangle(triangle(triangle(...triangle(256)...))) [256 trianglar] = triangle(triangle(triangle(...triangle(256²⁵⁶)...))) [255 trianglar] = triangle(triangle(triangle(...triangle(3.2 × 10⁶¹⁶)...))) [254 trianglar] = ...

Eller med den alternativa notationen:

mega = M(2,1,5) = M(256,256,3)

Med funktionen $f (x) = x x$ har vi mega = $f 256 (256) = f 258 (2)$ där exponenten representerar en funktionsexponent, inte en numerisk exponent.

Vi har (observera konvensionen att exponenter räknas från höger till vänster):

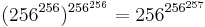
M(256,2,3) = $(256^{\,\!256})^{256^{256}}=256^{256^{257}}$
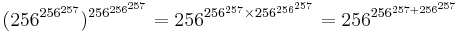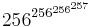
M(256,3,3) = $(256^{\,\!256^{257}})^{256^{256^{257}}}=256^{256^{257}\times 256^{256^{257}}}=256^{256^{257+256^{257}}}$ ≈ $256^{\,\!256^{256^{257}}}$

På samma sätt:

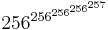
M(256,4,3) ≈ ${\,\!256^{256^{256^{256^{257}}}}}$
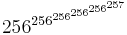
M(256,5,3) ≈ ${\,\!256^{256^{256^{256^{256^{257}}}}}}$

osv.

Således:

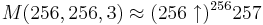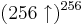mega = $M(256,256,3)\approx(256\uparrow)^{256}257$ , där $(256\uparrow)^{256}$ betecknar en funktionsexponent av funktionen $f (n) = 256 n$ .

Om vi avrundar lite mer grovt, (ersätter 257 i slutet av 256), får vi mega ≈ $256\uparrow\uparrow 257$ , (här används Knuths pilnotation).

Observera att efter dom första stegen så är värdet av $n n$ varje gång ungefär lika med $256 n$ . Faktum är att det är även ungefär lika med $10 n$ . Genom att använda exponenter med basen 10 får vi:

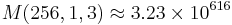
$M(256,1,3)\approx 3.23\times 10^{616}$
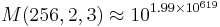$M(256,2,3)\approx10^{\,\!1.99\times 10^{619}}$ ( $log 10616$ är adderat med 616)
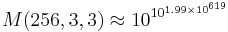$M(256,3,3)\approx10^{\,\!10^{1.99\times 10^{619}}}$ ( $619$ är adderat 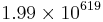$1.99\times 10^{619}$ , vilket är försumbart; därför är bara 10 adderat på slutet)

$M(256,4,3)\approx10^{\,\!10^{10^{1.99\times 10^{619}}}}$

...

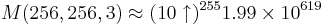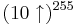mega = $M(256,256,3)\approx(10\uparrow)^{255}1.99\times 10^{619}$ , där $(10\uparrow)^{255}$ betecknar en funktionsexponent av funktionen $f (n) = 10 n$ . Alltså gäller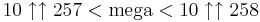 $10\uparrow\uparrow 257 < \mbox{mega} < 10\uparrow\uparrow 258$

Mosers tal

Det har bevisats att Mosers tal, trots att det är extremt stort, är mindre än Grahams tal.

Därför, med Conways kedjepilsnotation,

$\mbox{moser} < 3\rightarrow 3\rightarrow 65\rightarrow 2$

Steinhaus-Mosers notation

Från Rilpedia

Innehåll

Steinhaus polygonnotation

Alternativa notationer

Mega

Mosers tal

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk