M/S Askungen

Den följande diskussionen är ett arkiverat förslag om att radera nedanstående artikel. Var god och modifiera den inte. Senare kommentarer i ärendet bör göras på artikelns diskussionssida. Inga fler redigeringar bör göras nedan.

Resultatet av diskussionen blev Omskrivning Petter ☏ 24 juli 2006 kl.01.27 (CEST)

Aritmetisk serie

• • Anmälare: Petter ☏ 19 juli 2006 kl.23.28 (CEST)
  • Motivering: Det finns inget som heter så (se diskussion nedan).

Radera

Andreas Rejbrand 19 juli 2006 kl.23.36 (CEST) (alternativt byta namn till "aritmetisk följd" och sedan ändra ordet "serie" mot "följd" i artikeln)

Blankröst

1. Ulla 20 juli 2006 kl.23.16 (CEST) vet inget om detta

Behåll

1. RomanNose 19 juli 2006 kl.23.41 (CEST) (redir till aritmetisk talföljd)
2. E.G. 23 juli 2006 kl.10.45 (CEST) men skriv om enligt CÆSARs förslag nedan
3. Petter ☏ 23 juli 2006 kl.15.35 (CEST) Med nuvarande utseende kan den vara kvar.
4. Andreas Rejbrand 23 juli 2006 kl.15.46 (CEST) nya artikeltexten är en mycket trevlig bekantskap

Infoga

Diskussion
Det finns aritmetiska summor och talföljder. En serie är inom matematiken en summa med oändligt antal termer och en aritmetisk sådan konvergerar aldrig. Petter ☏ 19 juli 2006 kl.23.28 (CEST)

Jag har nu skapat aritmetisk följd, men en redirect dit vore missvisande. Petter ☏ 19 juli 2006 kl.23.41 (CEST)

RomanNose, en redirect vore missvisande eftersom en serie och en följd är två helt olika saker. Petter ☏ 19 juli 2006 kl.23.42 (CEST)

Instämmer fullt. Nog för att folk letar på fel ställen, men vi bör inte underblåsa missuppfattningar. --Andreas Rejbrand 19 juli 2006 kl.23.44 (CEST)

OK, då bör "aritmetisk serie" ändå sparas men beskrivas i artikeln istället --RomanNose 19 juli 2006 kl.23.46 (CEST)

Jag hittade detta, är det alltså fel? --RomanNose 19 juli 2006 kl.23.51 (CEST)

Ja, det är fel. Det framgår ganska tydligt att det som avses är en aritmetisk summa. Petter ☏ 19 juli 2006 kl.23.56 (CEST)

Nej, det vill jag inte påstå. Petter behandlar i sin premiss endast oändliga serier. Ändliga aritmetiska serier kan mycket väl konvergera (om de inte alltid gör det) och det finns en mycket känd och enkel formel för summan. --Andreas Rejbrand 19 juli 2006 kl.23.56 (CEST)

"Oändliga serier" är en tautologi. Alla serier är oändliga summor. Petter ☏ 19 juli 2006 kl.23.58 (CEST)

Beror nog lite på vem man frågar. Enligt Serie (matematik) verkar dock svwiki använda den definitionen, och då bör vi konsekvent skilja mellan summor och serier ("oändliga" summor). --Andreas Rejbrand 19 juli 2006 kl.23.59 (CEST)

Jag ändrade precis den artikeln så att det skulle bli rätt :-). Jag kontrollerat i två svenskspråkiga matteböcker av olika författare och i dem råder det ingen som helst tvivel om att en serie är en oändlig summa och ingenting annat. --Petter ☏ 20 juli 2006 kl.00.03 (CEST)

Och själv tittade jag just i en bok om analys, och samma definition används här. Dock är "slarv" med dessa begrepp mycket vanligt (om man nu väljer att kalla det direkt felaktigt). --Andreas Rejbrand 20 juli 2006 kl.00.05 (CEST)

WP bör väl inte uppmuntra till sådant slarv? Jag lade in två referenser i artikeln om serier. --Petter ☏ 20 juli 2006 kl.00.08 (CEST)

Nej, själv är jag mycket sträng beträffande noggrannhet, även om jag här inte riktigt är övertygad om att just restriktionen till "oändliga" summor är allmänt betraktad som den enda giltiga definitionen. Enwiki använder faktiskt begreppet "Arithmetic series" (en:Arithmetic_series) --Andreas Rejbrand 20 juli 2006 kl.00.10 (CEST)

Ja, i engelskan finns "series" och "infinite series". Så är inte fallet i svenskan. Här har vi "summa" och "serie". --Petter ☏ 20 juli 2006 kl.00.13 (CEST)

I Algebra och kombinatorik (tredje upplagan) av Anders Vretblad står "en aritmetisk serie är en summa av typen 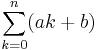, där a, b och n är givna tal". /81.229.39.209 20 juli 2006 kl.01.25 (CEST)

Om nu aritmetiska summor och aritmetiska följder kan sammanblandas med de icke existerande aritmetiska serierna, då är en sida som förklarar att uttrycket är felaktigt men ändå förekommande och "kan syfta på något av följande" den bästa lösningen. —CÆSAR ☢ 21 juli 2006 kl.12.41 (CEST)

Ja, eftersom uttrycket tydligen även förekommer i litteraturen så är det klokast så. Petter ☏ 21 juli 2006 kl.18.51 (CEST)

---

Den ovanstående diskussionen är ett arkiverat förslag om att radera ovanstående artikel. Var god och modifiera den inte. Senare kommentarer i ärendet bör göras på artikelns diskussionssida. Inga fler redigeringar bör göras ovan.