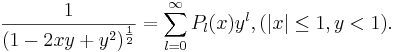Legendrepolynom

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Legendrepolynom, baser baserade på en speciell typ av polynom. Baserna Pl genereras från funktionen

\frac{1}{(1-2xy+y^2)^{1 \over 2}} = \sum_{l = 0}^{\infty}P_l(x)y^l, (|x| \le 1, y < 1).

Vänsterledet expanderas i baser av legendrepolynom, varav några termer i högerledet kan användas som dess approximation. Eftersom y < 1 används inom fysiken endast de första tre termerna: dessa motsvarar monopol (laddning), dipol och kvadrupol.

Polynomen kan genereras från följande rekursiva relation:

P0(x) = 1
P1(x) = x
P2(x) = (1/2)(3x2 - 1)
(l + 1)Pl+1(x) = (2l + 1)xPl(x) -lPl - 1(x),


Legendrepolynomen används bl.a. inom elektrostatik som baser för multipolutveckling av potentialen.

Hämtad från "https://sv.rilpedia.org/wiki/Legendrepolynom"
Personliga verktyg