Laplacetransformen av differentialekvationer
Från Rilpedia
Laplacetransformen ersätter differentialekvationer med algebraiska ekvationer och används för att lösa differentialekvationer med begynnelsevärden, utan att först behöva bestämma en allmän lösning och därefter använda begynnelsevärdena för att få fram den önskade lösningen. Detta är speciellt värdefullt när problemet är diskontinuerligt, och varje intervall måste behandlas för sig. I Laplacetransformens algebraiska ekvation blir istället varje intervall en term i ekvationen.
Definition
Laplacetransformen ersätter en funktion f(t) med en funktion F(s) där
Laplacetransformen av f kan också anges med 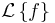 eller
eller 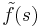 .
.
Man kan använda definitionen för att räkna Laplacetransformer, men det blir ofta krångliga uträkningar. I matematiska uppslagsverk och handböcker finns tabeller över Laplacetransformer för en mängd vanliga funktioner.