Kontravariant vektor
Från Rilpedia
Kontravariant vektor kallas inom allmän relativitetsteori en vektor med index uppe,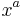 
. Att en vektor har index uppe eller nere har enbart matematisk betydelse.
En kontravariant vektor transformeras genom multiplikation med (proportionellt mot) skalan.
Lägg ett koordinatsystem (x,y) i verkligheten och ett (x',y') på en karta i skala 1:1000 = 0,001. Då blir 1 m i verkligheten 1 mm på kartan. Hastigheten 1 m/s blir 1 mm/s på kartan och lufttryckgradienten 1 pa/m blir 1 Pa/mm.
När man transformerar hastighet från verklighet till karta multiplicerar man alltså med skalan 1*0,001 m/s = 1 mm/s.
När man transformerar lufttrycksgradient från verklighet till karta dividerar man med skalan (omvänd proportionalitet) 1/0,001 Pa/m = 1 Pa/mm.
Hastighet är ett exempel på en kontravariant vektor, lufttryckgradient är ett exempel på en kovariant vektor.
För att bestämma skalan i x-riktningen kan man gå ett steg (δx) i verkligheten och se vad det motsvarar på kartan (δx'). Kartans skala är då δx'/δx i x-riktningen och på motsvarande sätt δy'/δy i y-riktningen.
En vektor är entydigt bestämd av sina axelkomposanter. Transformation till ett annat koordinatsystem kan alltså göras genom att man delar upp vektorn i dess axelkomposanter och transformerar axelkomposanterna.
För den kontravarianta vektorn A gäller då (om kartans axlar är parallella med verklighetens
Ax' = Ax δx'/δx
Ay' = Ay δy'/δy
och för den kovarianta vektorn B gäller
Bx' = Bx δx/δx'
By' = By δy/δy'
Om kartans axlar inte är parallella med verklighetens ersätta detta av
Ax' = Ax δx'/δx + Ay δx'/δy
Ay' = Ax δy'/δx + Ay δy'/δy
och för den kovarianta vektorn B gäller
Bx' = Bx δx/δx' + By δy/δx'
By' = Bx δx/δy' + By δy/δy'
I ett kroklinjigt koordinatsystem behöver inte axeltangenterna sammanfalla med normalerna till koordinatytorna. En vektors projektioner på axeltangenterna kallas då "vektorns kontravarianta komposanter" och vektorns projektioner på koordinatytenormalerna kallas "vektorns kovarianta komposanter".
