Från Rilpedia

Skall inte förväxlas med komplexa tal.

Komplexitet används för att tala om hur resurskrävande en algoritm eller en funktion är. Normalt analyseras endast det asymptotiska beteendet, och inte bidrag av lägre ordning. För att kunna bedöma komplexiteten hos ett problem måste man först bestämma sig för vilken kostnadsmodell som ska användas. I princip så anger man komplexitet som en funktion av indatats storlek. Man bestämmer först vad storleken av indatan lämpligen mäts i. Därefter tilldelar man kostnader till de grundläggande operationerna i problemet. Är man bara intresserad av den asymptotiska komplexiteten så räcker det att avgöra hur en operations kostnad beror på storleken av indatan. Normalt söker man värsta-falls-komplexiteten, det vill säga komplexiteten för sämst utformade indata. För vissa algoritmer är dock medelkomplexiteten också av intresse.

Inom datorprogrammering finns mätmetoder för att kvantitativt bestämma komplexitet av en metod/funktion eller en modul/klass:

• McCabe-tal, eller cyklomatisk komplexitet, som anger antal vägar genom en metod
• Efferent Couplings, antal beroenden till andra metoder, moduler eller klasser (till exempel referenser till externa data, metoder etc.)
• Infferent Couplings, antal beroenden från andra metoder, moduler eller klasser (till exempel referenser till externa data, metoder etc.)
• antal rader kod per metod, klass/modul
• arvsdjup (för klasser)

Komplexitet kan även användas för att tala om hur resurskrävande ett specifikt problem, till exempel sortering, är. Man är då intresserad av att dels försöka hitta en undre gräns till ett problems komplexitet, och dels en övre gräns. Om dessa båda gränser överensstämmer så vet man problemets komplexitet. Att bestämma en övre gräns är enkelt. Det räcker att hitta på en algoritm, och beräkna dess komplexitet. Den lägsta komplexitet man känner för en algoritm att lösa ett problem utgör en övre gräns för problemets komplexitet. För att bestämma en undre gräns krävs ofta avancerade matematiska beräkningar, eller så får man ta till någon trivial undre gräns.

Exempel

En mycket enkel algoritm för att multiplicera två positiva tal, a och b är: Låt a vara det största av talen och b det minsta talet och beräkna 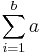. Indatan är här de båda talen a och b. Vi genomför två operationer: jämförelse och summering. Summering kan ses som en serie enkla additioner av två tal. Att addera två tal är enkelt, och vi kan säga att det har en konstant kostnad, C₁. Även att jämföra två tal är enkelt och har också konstant kostnad, C₂. Att utföra samma typ av beräkning, med kostnad C₁ b gånger kostar 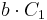. Den totala kostnaden för multiplikationen blir då 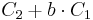. Vi har här valt b som mått på indatans storlek under beräkningens gång genom att inse att det som påverkar kostnaden endast beror av b. Vår algoritm har alltså komplexiteten .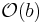