Von Kochs kurva
Från Rilpedia
von Kochs kurva, även känd som Koch-kurvan eller snöflingekurvan, beskrevs av matematikern Helge von Koch i en uppsats med titeln "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire", publicerad år 1904 i Arkiv för matematik, astronomi och fysik. Syftet med uppsatsen var att ge ett geometriskt mer tilltalande exempel på en kontinuerlig kurva som saknar tangent i alla punkter, än det som Karl Weierstrass upptäckte 1861. Numera är Koch-kurvan även känd för att vara en av de först beskrivna fraktalerna, ett begrepp som myntades först 70 år senare.
Koch-kurvans definition:
- Tag en linje.
- Dela linjen i tre lika stora delar.
- Gör en kopia av den mellersta delen.
- Sätt upp de två kopiorna i vinkel mot varandra så att de får plats inom samma sträcka som en ensam linje annars gör.
- Upprepa (iterera) från steg 2 för alla de nya linjer som uppkommit av operationen.
Antalet nya linjer att operera på blir hela tiden 4 gånger tidigare antal linjer, så antalet linjer efter n iterationer blir följaktligen 4n. Linjen ökar sin längd med en tredjedel i varje ny iteration och kommer sålunda till slut att bli en oändligt lång kurva men inom en begränsad yta. Därför är kurvans dimensionstal inte ett heltal. Det här är anledningen till att Koch-kurvan är en fraktal, (av lat; fractus, bråkdel). Koch-kurvans Hausdorffdimension är 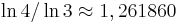 .
.
von Kochs snöflinga
Denna figur erhålls genom att man börjar med en liksidig triangel istället för bara en linje. Vid varje iteration ökar omkretsen med en tredjedel. I iteration n är längden (4 / 3)n gånger ursprungslängden. Snöflingans omkrets saknar alltså gränsvärde och går mot oändligheten när n går mot oändligheten. Däremot konvergerar dess area mot 8/5 gånger ursprungstriangelns area.
Programexempel
Följande är en algoritm i programspråket QBasic som visar von Kochs kurva som en IFS-fraktal. Koden är nog inte allt för svår att översätta till C/C++ eller något annat högnivåspråk förutsatt att man vet hur man gör för att skapa en skärmyta och skriver pixlar till den. Notera då att tecknet [#] motsvarar float i C och [%] är int.
SCREEN 12 RANDOMIZE TIMER rad# = ATN(1#) / 45# vinkel# = 60# * rad# skalning# = 1# / 3# bildskalning# = 200# positionx#(0) = 1# positiony#(0) = 0# positionx#(1) = COS(vinkel#) / 2# positiony#(1) = SIN(vinkel#) / 2# rotationx#(0) = skalning# rotationy#(0) = 0# rotationx#(1) = COS(vinkel#) * skalning# rotationy#(1) = -SIN(vinkel#) * skalning# x# = 0.75# y# = 0# WHILE INKEY$ = "" i% = FIX(RND * 2) t# = rotationx#(i%) * x# - rotationy#(i%) * y# + positionx#(i%) y# = rotationx#(i%) * y# + rotationy#(i%) * x# + positiony#(i%) IF FIX(RND * 2) THEN x# = t# ELSE x# = -t# PSET (320 + bildskalning# * x#, 240 - bildskalning# * y#) WEND END
Externa länkar
- Wikimedia Commons har media som rör Von Kochs kurva
- Sök ytterligare bilder på Koch-kurvan, (med Google)





