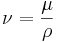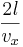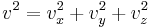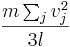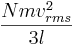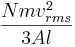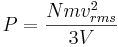Kinetiska gasteorin
Från Rilpedia
Kinetiska gasteorin förklarar de makroskopiska egenskaperna för gaser med iakttagande av deras natur på en molekylär nivå.
Innehåll |
Grundpriciper
De fundamentala principerna för kinetisk teori finns angivna i form av flera grundprinciper:
- Gaser är uppbyggda av atomer (ädelgaser) eller molekyler som rör sig i en konstant slumpartad rörelse. De rörliga partiklarna kolliderar med varandra och med väggarna på en behållare.
- Kollisionen mellan partiklarna är elastisk.
- Den totala volymen av gasmolekylerna är försumbar i förhållande till behållarens volym.
- Dragningskraften mellan molekylerna är försumbar.
Ovan angivna förutsättningar gäller en ideal gas. Verklig gas närmar sig det ideala stadiet vid låg densitet och hög temperatur.
Tryck
Tryck förklaras av den kinetiska teorin av att det uppstår av gasmolekyler som krockar med behållarens väggar. Härledningen för den matematiska formeln följer här:
Antag att en gas med n molekyler, varje med en massa m är instängda i en behållare med volymen V. Antag vidare att en gasmolekyl kolliderar med en vägg på behållaren som är vinkelrät mot x-axeln och därefter studsar iväg i motsatt riktning och med samma hastighet (en elastisk kollision). Då är partikelns förlorade rörelseenergi lika med:
- 2mvx
där vx är x-värdet för den initiala hastigheten hos partikeln.
Kraften är med den takt vilken rörelseenergin ändras. Om man beaktar en partikels krockar med väggen varje
tidsenhet där l är längden av behållaren.
Eftersom partiklarna rör sig slumpartat i alla riktningar och eftersom
gäller för varje partikel, gäller för den totala kraften
Detta kan skrivas som
där vrms är rms hastigheten för gasen.
Därför är trycket – kraften per areaenhet lika med
där A är väggens area.
Så har vi fått följande uttryck för tryck
Detta resultat är intressant och betydelsefullt eftersom det relaterar tryck, i ett makroskopiskt perspektiv, till den genomsnittligt överensstämmande kinetiska energin per molekyl: 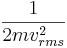 , vilket är i ett mikroskopiskt perspektiv.
, vilket är i ett mikroskopiskt perspektiv.
Notera även att produkten av tryck och volym bara är 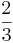 av den totala kinetiska energin.
av den totala kinetiska energin.
Temperatur
Ekvationen här ovan talar om att produkten av tryck och volym per mol är proportionerlig med medelvärdet för den kinetiska energin. Vidare säger den ideala gaslagen att denna produkt är proportionell mot den absoluta temperaturen. Tillsammans avslöjar dessa två uppgifter en viktig sak gällande den kinetiska teorin: Den genomsnittliga kinetiska energin är proportionell mot den absoluta temperaturen. Konstanten för proportionaliteten är 2/3 av Boltzmanns konstant, vilket är förhållandet mellan gaskonstanten R och Avogadros tal (oavsett typ av gas). Detta resultat är relaterat till ekvipartitionsteoremet.
Då den kinetiska energin per kelvin är:
då är den kinetiska energin vid 273,15 K:
- per mol 3406 J
- per molekyl 5,65 zJ = 35,2 meV.
Exempel:
- Väte (molekylmassa 2 u): 1703 kJ/kg
- Kväve (molekylmassa 28 u): 122 kJ/kg
- Syre (molekylmassa 32 u): 106 kJ/kg
RMS-hastigheten för molekyler etc.
Den kinetiska energiformeln ger:
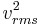 = 24,940 T / molekylmassa
= 24,940 T / molekylmassa
med v i m/s och T i kelvin.
För normaltemperatur är RMS-hastigheten:
- Fria neutroner 2610 m/s
- Väte 1846 m/s
- Kväve 493 m/s
- Syre 461 m/s
Den mest sannolika hastigheten är 81,6 % av dessa (alltså 2131 m/s för fria neutroner), och medelhastigheten 92,1 %, se även Maxwell-Boltzmannfördelning.
Newton
- Skjuvspänningen i gaser:
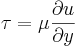
- Kinetisk viskositet i gaser: