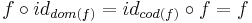Från Rilpedia

För begreppet kategori inom filosofi, se Kategori (filosofi), för klassificering av Wikipediaartiklar, se Rilpedia:Kategori.

Inom matematiken utgör en kategori en struktur bestående av en uppsättning objekt, en uppsättning morfismer och två tillordningar; ett (domän-) objekt; dom(f), och ett (kodomän-) objekt; cod(f), till varje morfism f. Till kategoristrukturen kommer också en tillordning av en (identitets-) morfism, id_x, till varje objekt x, uppfyllande

dom(id_x) = cod(id_x) = x

samt en partiell binär kompositionsoperation, 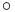, på morfismer, betecknad 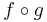och definierad för alla par av morfismer f och g sådana att cod(g) = dom(f), uppfyllande

för alla morfismer f, och

för alla morfismer f, g, h där komposition är definierad.

En morfism f sägs gå från objektet dom(f) till objektet cod(f). Morfismerna utgör på så vis bågar i en riktad graf där objekten utgör hörn. För två objekt x och y betecknar Mor(x, y) uppsättningen av alla morfismer där domän-objektet är x och kodomän-objektet är y.

För att utan självmotsägelser kunna använda kategoriteoretiska begrepp i resonemang kring med mängdlärans storheter görs distinktioner mellan olika kategorier baserat på om de är små eller stora. Med en "liten" kategori avses en kategori där uppsättningen morfismer utgör en mängd. Med en kategori utan särskild storleksangivelse avses en kategori där uppsättningen morfismer utgör en äkta klass, men där uppsättningen morfismer från vilket objekt som helst, x, till vilket annat objekt som helst, y, alltid utgör en mängd. Med en stor kategori avses en kategori där uppsättningen morfismer utgör en metaklass och uppsättningen morfismer från ett objekt till ett annat, Mor(x,y), utgör en klass.

Särskilda typer av kategorier är:

• kategorier med ett terminalt objekt
• kategorier med ett initialt objekt
• kategorier med produkt
• kategorier med summa
• kartesiskt slutna kategorier