Jordans lemma
Från Rilpedia
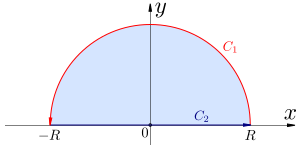
Jordans lemma är ett resultat inom komplex analys som ofta används vid beräkning av kurvintegraler.
Det finns flera olika varianter på exakt hur Jordans lemma ser ut, men en av dessa kan användas för att visa flera andra: Om C1 är övre halvcirkeln med radien R, gäller att
Med hjälp av detta kan man visa att om 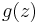 är en funktion sådan att
är en funktion sådan att 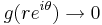 då
då 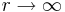 för alla
för alla ![\theta\in [0,\pi]](/w/images/sv.rilpedia.org/math/1/b/9/1b98c8d3d657d452f7a2a09caf0d00fb.png) (till exempel om
(till exempel om 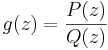 där P och Q är två polynom sådana att grad Q > grad P) så gäller att
där P och Q är två polynom sådana att grad Q > grad P) så gäller att
Tillämpningar
En vanlig tillämpning av Jordans lemma är att bestämma integralen av en funktion f på hela 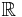 , eftersom kurvintegralen kring C kan skrivas:
, eftersom kurvintegralen kring C kan skrivas:
där C2 är en del av den reella axeln. Om man nu låter radien på C gå mot oändligheten, kommer C2 gå mot hela 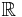 . Om f är en funktion så att
. Om f är en funktion så att 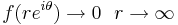 , kommer första integralen, enligt ovan, gå mot noll så att:
, kommer första integralen, enligt ovan, gå mot noll så att:
och integralen i vänsterledet kan räknas ut med residysatsen, uttryckt som:
där summan tas över alla residyer i övre komplexa halvplanet (den reella axeln exkluderad).
Källor
- Stephen D. Fisher: Complex Variables, 1999. ISBN 0-486-40679-2.




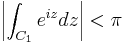
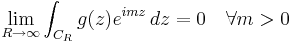
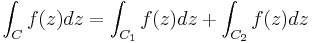
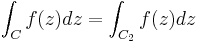
![\int_{-\infty}^\infty f(x)dx = 2 \pi i \sum Res[f(x)]](/w/images/sv.rilpedia.org/math/f/c/f/fcf425a54b66d44bb089fe4415b89fc3.png)