Raoults lag
Från Rilpedia
Raoults lag säger att partialtrycket för en gas i en vätskeblandning är lika med mättnadsångtrycket för gasen i dess rena form multiplicerat med molbråket för gasen i vätskeblandningen (dvs hur stor andel som gasen utgör i vätskeblandningen, i mol/mol):
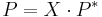
där P = partialtrycket (oftast uttryckt i bar), X är molbråket för gasen i vätskeblandningen, och P* är mättnadsångtrycket (i bar). Gasen antas här vara ideal, vilket bl.a. innebär att partialtrycket = fugaciteten.
Innehåll |
Ideal lösning
En ideal lösning definieras som en vätskeblandning som uppfyller Raoults lag. För att detta ska vara möjligt måste varje komponent i vätskeblandningen uppvisa exakt samma interaktioner med andra komponenters molekyler som med andra molekyler för den rena komponenten. Detta är nästan aldrig fallet utom då komponenterna i vätskeblandningen är mycket lika varandra (vissa blandningar av organiska lösningsmedel kan uppfylla kriteriet), och därför är ett antagande om ideal lösning oftast ett dåligt antagande.
När uppfylls Raoults lag respektive Henrys lag?
Trots att mycket få vätskeblandningar är ideala lösningar finns ändå omständigheter då Raoults lag är giltig i samtliga fall. I vätskeblandningar med en komponent som dominerar kommer Raoults lag att gälla ungefärligt för den dominerande komponenten eftersom partialtrycket då närmar sig mättnadsångtrycket. För komponenter med låga molbråk måste vi däremot införa en aktivitetskoefficient γ, som beskriver avvikelsen från en ideal lösning. Denna aktivitetskoefficient multiplicerat med mättnadsångtrycket är i själva verket en form av Henrys lags konstant. Alltså:
| Då X → 1: | P → P* | Raoults lag gäller, Henrys lag gäller ej |
| Då X → 0: | P → γXP* | Raoults lag gäller ej, Henrys lag gäller |
Se även
Litteratur
- Environmental organic chemistry. 2003. R.P. Schwarzenbach, P.M. Gschwend & D.M. Imboden. Wiley.



