Homotopi
Från Rilpedia
(Omdirigerad från Homotopiklass)
Homotopi är ett begrepp inom topologi.
Låt U och V vara topologiska rum. Två funktioner f, 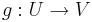 säges vara homotopa om det finns en kontinuerlig funktion
säges vara homotopa om det finns en kontinuerlig funktion ![F : U \times [0, 1] \to V](/w/images/sv.rilpedia.org/math/b/c/d/bcda6e4e96a1331a1a37d17e466e16ed.png) , där
, där 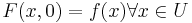 , och
, och 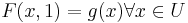 . Funktionen F är en homotopi.
. Funktionen F är en homotopi.
I fallet ![U = [0, 1] (\subset \mathbb{R})](/w/images/sv.rilpedia.org/math/d/7/a/d7a5fdb910b93421f7132c0f675d3483.png) ,
, 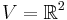 , är alltså två funktioner homotopa om kurvorna i
, är alltså två funktioner homotopa om kurvorna i 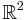 de beskriver kan kontinuerligt deformeras till varandra.
de beskriver kan kontinuerligt deformeras till varandra.
Relationen mellan funktioner 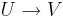 att vara homotopa är en ekvivalensrelation, som delar in funktionerna i homotopiklasser.
att vara homotopa är en ekvivalensrelation, som delar in funktionerna i homotopiklasser.



