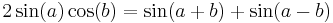Heterodynprincipen
Från Rilpedia
Heterodynprincipen behandlar elektriska svängningar. Den säger att två olika frekvenser som blandas multiplikativt ger upphov till två nya frekvenser som är summan respektive skillnaden av de ursprungliga. Av frekvenserna f1 och f2 får man alltså f1+ f2 och | f1– f2|. Om signaler på 4 och 5 MHz blandas multiplikativt, skapas 1 och 9 MHz.
Multiplikativ blandning innebär att det inte räcker att bara addera de två signalerna linjärt som i en vanlig ljudmixer. De måste multipliceras eller åtminstone blandas i en olinjär process så att den ena signalens närvaro har betydelse för hur den andra hanteras.
Heterodynprincipen används mycket flitigt i radio- och TV-mottagare som därför kallas superheterodynmottagare.
Det mänskliga örat är inte helt linjärt. När man lyssnar på två toner kan örat uppfinna svaga toner som inte finns i verkligheten. De kallas kombinationstoner eller spöktoner och uppkommer i enlighet med heterodynprincipen. Örats olinjaritet innebär inte en perfekt multiplikation av tonerna, varför mer än två nya toner kan skapas. Bäst hörs skillnadsfrekvenserna f2– f1 samt 2f1– f2 (där f2 har högre frekvens än f1). Effekten blir tydligast med rena sinustoner. Vissa gamla orglar utnyttjade detta medvetet för att skapa fiktiva bastoner utan de stora baspipor som annars hade behövts.
Matematisk förklaring
Ur de grundläggande trigonometriska sambanden för addition och subtraktion av två vinklar a och b får vi
Vi kan betrakta ekvationen som en ögonblicksbild av ett förlopp där vinklarna a och b växer varv efter varv med olika hastighet medan tiden går. Varje sin- och cos-uttryck beskriver då en enkel harmonisk svängning mellan amplitudvärdena 1 och –1 där vinkeln i parentesen beror på svängningens frekvens.
Ekvationen säger oss då att multiplikation av två svängningar med frekvenser som motsvarar a och b ger oss två nya svängningar med frekvenser som motsvarar a+b och a–b. Om b skulle vara större än a, går det utmärkt att använda b–a istället för a–b. Det ändrar ett tecken i ekvationen, men svängningarnas frekvenser förblir desamma.