Hamiltongrafer
Från Rilpedia
Hamiltongrafer är det gemensamma namnet för grafer som har hamiltoncyklar/vägar i dem. Hamiltonväg är en väg i en graf som innehåller varje hörn (nod, punkt) en gång. En hamiltoncykel är en cykel som innehåller varje hörn en gång och återvänder till samma startpunkt.
Hamiltongrafer har många tillämpningar, bl.a. handelsresandeproblemet och springareproblemet.
Innehåll |
Historia
Hamiltongrafer är uppkallade efter William Rowan Hamilton som bl.a. uppfann Icosianspelet. Han sålde idéen vidare till en leksaksaffärsman i Dublin. Hamilton löste detta problem med hjälp av vad han kallade Icosian calculus. Frågan som återstod var, vilka vilkor krävs det för att en graf ska ha en hamiltoncykel? Än så länge finns det inget fullständigt sätt att bevisa att det finns en hamiltoncykel i en graf. Men det finns satser som anses vara godtyckliga att visa att grafen kan innehålla hamiltoncyklar.
Matematiska Egenskaper
Definitioner
Först följer några definitioner inom grafteori och sedan några intressanta satser gällande hamiltoncyklar.
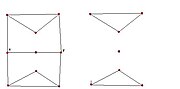
- En väg inom grafteori är ett ändligt följd av hörn där det finns förbindelse mellan dem i form av s.k. bågar eller kanter. I grafen till vänster är ett exempel på en väg (a , f, e , c).
- En cykel är en väg som kommer tillbaks till startpunkten. Ett exempel på grafen till vänster är (c, d, e, c)
- Antalet kanter som förbinder hörnen till resten av grafen kallas hörnens grad. Det betecknas som d(vn) där vn är hörnen. Exempel på grafen till vänster är att hörnen a har grad 2:
d(a) = 2
Den formella definitionen av en hamiltonväg/cykel är som följande:
Låt G vara en graf med fler än 2 hörn. Vi säger att grafen G har en Hamiltonväg/cykel om det finns en väg/cykel som omfattar alla hörnen i grafen.
Ett exempel på en hamiltonväg på grafen till vänster är (b, a, f, e, c, d) Ett exempel på en hamiltoncykel på grafen till vänster är (a, b, c, d, e, f, a)
Satser
Det finns än så länge inget ordentligt sätt att bevisa att det finns en hamiltonväg i en graf. Man kan, åt andra sidan, visa att graf inte har en hamiltoncykel. Detta förklaras av följande sats.
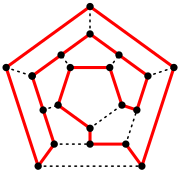
[1] "Låt G vara en enkel graf. Antag att det finns k st hörn v1,v2,...,vk i G sådana att om man tar bort dessa hörn och alla de kanter, som har hörnen som ändpunkter, så får man en graf med minst k + 1 sammanhängande komponenter. Då kan inte G innehålla någon hamiltoncykel."[1]
Ett exempel på föregående sats är grafen till höger. Om man tar bort hörnen markerad x och y blir det 2 + 1 osammanhängande delar vilket, enligt satsen visar att grafen inte har några hamiltoncyklar i den.
Det finns satser som anger tillräckligt med vilkor för att det ska finnas en hamiltoncykel. Följande sats bevisades av G. A. Dirac 1952.
[2] Låt G vara en enkel graf med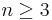 
hörn. Om graden av varje hörn är minst 
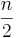innehåller grafen en hamiltoncykel. [2]
Att hitta en hamiltoncykel klassas som en NP-komplett problem. Det betyder att lösningen kan vara väldigt tidskrävande om man jobbar med stora grafer.
Tillämpningar
Hamiltongrafer har fått en större betydelse med datorns tillkomst där större beräkningar kan göras på kortare tid. Tillämpningarna är många, t.ex. optimering, geometri och logistik. Hamiltongrafer används inom beräkningar inom turnering och Cayley grafer.[3]
_tree_seartch_P0.gif)
Handelsresandeproblemet
Det är inte alltid intressant att veta om det finns en hamiltoncykel, utan vilken hamiltoncykel kostar minst. Det gör man på grafer som har givna bågkostnader. Se exempel till höger. Detta brukar kallas för ett gemensamt ord; handelsresandeproblemet. Bågkostnader kan representera många olika saker; tid, sträckor, kostnad, osv.
Det är oftast svårt att hitta den minsta kostnaden för en cykel eftersom sökandet kan bli väldigt tidskrävande beroende på storleken av grafen. Man har istället utformat algoritmer som kan hitta någon cykel, vilket går betydligt fortare, men man vet inte om det faktiskt är den kortaste vägen eller inte. Detta kallas en heuristik metod.
Springareproblemet
Är det möjligt för springaren i schack att gå på varje ruta exakt en gång på schackbrädan?
Detta är en fråga från antiken som klassas som en svår uppgift. Den första algoritmen för att lösa springareproblemet var Warnsdorffs algoritm i 1823 av H. C. Warnsdorff.
En enkel sammanfattning av Warnsdorffs lösning är att det gäller att välja den rutan som har så få drag från den som möjligt. Detta är för att inte skapa en återvändsgränd så att springaren inte kan gå på någon annan rutan än den, den har redan gått på.
Källor
- ↑ A. Asratian; A. Björn; B. O. Turesson: Diskret matematik 2008 Matematiska Instutitionen, Linköping
- ↑ Andrásfai Béla: Introductory Graph Theory 1977 Akadémiai Kiadó, Budapest ISBN 0 85274 249 5
- ↑ Edited by Alspach B.R.; Godsil C.D. : Cycles in Graphs 1985 Elsevier Science Publishers B.V.
