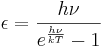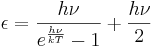Guide:Nollpunktsenergi/ZPE
Från Rilpedia
In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system. The concept of zero-point energy was proposed by Albert Einstein and Otto Stern in 1913, which they originally called "residual energy" or Nullpunktsenergie. All quantum mechanical systems have a zero point energy. The term arises commonly in reference to the ground state of the quantum harmonic oscillator and its null oscillations. In quantum field theory, it is a synonym for the vacuum energy, an amount of energy associated with the vacuum of empty space. In cosmology, the vacuum energy is taken to be the origin of the cosmological constant. Experimentally, the zero-point energy of the vacuum leads directly to the Casimir effect, and is directly observable in nanoscale devices.
Because zero point energy is the lowest possible energy a system can have, this energy cannot be removed from the system.
Despite the definition, the concept of zero-point energy, and the hint of a possibility of extracting "free energy" from the vacuum, has attracted the attention of amateur inventors. Numerous perpetual motion and other pseudoscientific devices, often called free energy devices, exploiting the idea, have been proposed. As a result of this activity, and its intriguing theoretical explanation, it has taken on a life of its own in popular culture, appearing in science fiction books, games and movies.
Innehåll |
History
In 1900, Max Planck derived the formula for the energy of a single "energy radiator", i.e. a vibrating atomic unit, as:
In 1913, using this formula as a basis, Albert Einstein and Otto Stern published a paper of great significance in which they suggested for the first time the existence of a residual energy that all oscillators have at absolute zero. They called this "residual energy" and then Nullpunktsenergie (in German), which later became translated as zero-point energy. They carried out an analysis of the specific heat of hydrogen gas at low temperature, and concluded that the data are best represented if the vibrational energy is taken to have the form:[1]
Thus, according to this expression, even at absolute zero the energy of an atomic system has the value ½hν.
Foundational physics
In classical physics, the energy of a system is relative, and is defined only in relation to some given state (often called reference state). Typically, one might associate a motionless system with zero energy, although doing so is purely arbitrary.
In quantum physics, it is natural to associate the energy with the expectation value of a certain operator, the Hamiltonian of the system. For almost all quantum-mechanical systems, the lowest possible expectation value that this operator can obtain is not zero; this lowest possible value is called the zero-point energy. (Caveat: If we add an arbitrary constant to the Hamiltonian, we get another theory which is physically equivalent to the previous Hamiltonian. Because of this, only relative energy is observable, not the absolute energy.)
The origin of a minimal energy that isn't zero can be intuitively understood in terms of the Heisenberg uncertainty principle. This principle states that the position and the momentum of a quantum mechanical particle cannot both be known arbitrarily accurately. If the particle is confined to a potential well, then its position is at least partly known: it must be within the well. Thus, one may deduce that within the well, the particle cannot have zero momentum, as otherwise the uncertainty principle would be violated. Because the kinetic energy of a moving particle is proportional to the square of its velocity, it cannot be zero either. This example, however, is not applicable to a free particle - the kinetic energy of which can be zero.
Varieties of zero-point energy
The idea of zero-point energy occurs in a number of situations, and it is important to distinguish these, and note that there are many closely related concepts.
In ordinary quantum mechanics, the zero-point energy is the energy associated with the ground state of the system. The most famous such example is the energy 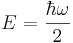 associated with the ground state of the quantum harmonic oscillator. More precisely, the zero-point energy is the expectation value of the Hamiltonian of the system.
associated with the ground state of the quantum harmonic oscillator. More precisely, the zero-point energy is the expectation value of the Hamiltonian of the system.
In quantum field theory, the fabric of space is visualized as consisting of fields, with the field at every point in space and time being a quantized simple harmonic oscillator, with neighboring oscillators interacting. In this case, one has a contribution of 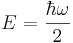 from every point in space, resulting in a technically infinite zero-point energy. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
from every point in space, resulting in a technically infinite zero-point energy. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.
In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations or the zero-point energy to the particle masses.
Experimental evidence
The simplest experimental evidence for the existence of zero-point energy in quantum field theory is the Casimir effect. This effect was proposed in 1948 by Dutch physicist Hendrik B. G. Casimir, who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. A small force can be measured between the plates, which is directly ascribable to a change of the zero-point energy of the electromagnetic field between the plates.
Although the Casimir effect at first proved hard to measure, because its effects can be seen only at very small distances, the effect is taking on increasing importance in nanotechnology. Not only is the Casimir effect easily and accurately measured in specially designed nanoscale devices, but it increasingly needs to be taken into account in the design and manufacturing processes of small devices. It can exert significant forces and stress on nanoscale devices, causing them to bend, twist, stick and break.
Other experimental evidence includes spontaneous emissions of light (photons) by atoms and nuclei, observed Lamb shift of positions of energy levels of atoms, anomalous value of electron's gyromagnetic ratio, etc.
Gravitation and cosmology
| Unsolved problem in physics: Why doesn't the zero-point energy of vacuum cause a large cosmological constant? What cancels it out?
(more unsolved problems in physics) |
In cosmology, the zero-point energy offers an intriguing possibility for explaining the speculative positive values of the proposed cosmological constant. In brief, if the energy is "really there", then it should exert a gravitational force. In general relativity, mass and energy are equivalent; either produces a gravitational field.
One obvious difficulty with this association is that the zero-point energy of the vacuum is absurdly large. Naively, it is infinite, but one must argue that new physics takes over at the Planck scale, and so its growth is cut off at that point. Even so, what remains is so large that it would visibly bend space, and thus, there seems to be a contradiction. There is no easy way out, and reconciling the seemingly huge zero-point energy of space with the observed zero or small cosmological constant has become one of the important problems in theoretical physics, and has become a criterion by which to judge a candidate Theory of Everything.
Propulsion theories
Another area of research in the field of zero point energy is how it could be used for propulsion. NASA and British Aerospace both have programs running to this end though practical technology is still a long way off. For any success in this area, it would have to be possible to create repulsive effects in the quantum vacuum, which according to theory should be possible and experiments to produce and measure these effects are planned for the future.
Rueda, Haisch and Puthoff[2][3][4] have proposed that an accelerated massive object interacts with the zero point field to produce an electromagnetic drag force which gives rise to the phenomenon of inertia; see stochastic electrodynamics.
"Free energy" devices
The Casimir effect has established zero point energy as an uncontroversial and scientifically accepted phenomenon. However, the term zero point energy has also become associated with a highly controversial area of human endeavour - the design and invention of so-called "free energy" devices, similar to perpetual motion machines in the past.
Related patents
- U.S. Patent 5 590 031 ~ System for converting electromagnetic radiation energy to electrical energy
See also
- Quantum harmonic oscillator
- Vacuum energy
- Radiant energy
- Unruh effect
- Zero-point energy in popular culture
- Dark energy
References
- ↑ Laidler, Keith, J. (2001). The World of Physical Chemistry. Oxford University Press. ISBN 0198559194.
- ↑ Haisch, Bernard; Alphonso Rueda, H.E. Puthoff (February 1994). "Inertia as a zero-point-field Lorentz force". Physical Review A 49 (2): 678-694.
- ↑ Rueda, Alfonso; Bernhard Haisch (1998). "Contribution to inertial mass by reaction of the vacuum to accelerated motion". Found.Phys. 28: 1057-1108.
- ↑ Rueda, Alfonso; Bernhard Haisch (1998). "Inertia as reaction of the vacuum to accelerated motion". Phys.Lett. A240: 115-126.
- Beiser, Arthur (1967). Concepts of Modern Physics. McGraw-Hill.
- Albert Einstein and L. Hopf (1910). "On a theorem of the probability calculus and its application to the theory of radiation". Ann. Phys. 33: 1096–1104.
- Albert Einstein and L. Hopf (1910). "Statistical investigation of a resonator’ s motion in a radiation field". Ann. Phys. 33: 1105–1115.
- Albert Einstein and Otto Stern, (1913). "—". Ann. Phys. 40: 551.
- Forward, R. (1984). "Extracting electrical energy from the vacuum by cohesion of charged foliated conductors". Phys. Rev. B 30: 1700.
- Bernard Haisch, Alfonso Rueda and York Dobyns (2001). "Inertial mass and the quantum vacuum fields". Annalen der Physik 10: 393-414.
- Loudon, R. (September 2000). The Quantum Theory of Light, Third Edition, Oxford: Clarendon Press. ISBN 0-19-850176-5.
- Milonni, Peter W. (1994). The Quantum Vacuum: an Introduction to Quantum Electrodynamics. New York: Academic. ISBN 0-12-498080-5.
- Nernst, W. (1916). "—". Verh. Deutsch Phys. Ges. 18: 83.
- Alfonso Rueda and Bernard Haisch (2005). "Gravity and the Quantum Vacuum Inertia Hypothesis". Annalen der Physik 14: 479-498.
- Sciama, D. W. (1991). in Simon Saunders and Henry R. Brown, eds: The Philosophy of Vacuum. Oxford: Clarendon Press. ISBN 0-19-824449-5.
External links
- Zero-point energy? "Ask the Van" popular science FAQ at University of Illinois.
- Philip Yam, "Exploiting Zero-point Energy", Scientific American Magazine, December 1997, pp. 82-85.
- Alokik Kanwal, Zero-point energy (Power Point presentation; rutgers.edu)