Gitter (grupp)

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
De fem två-dimensionala Bravaisgitter: 1) skev, 2) rektangular, 3) centrerat rektangulär, 4) hexagonal, 5) fyrkant.

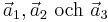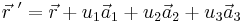Gitter är en uppsättning ordnade matematiska punkter. Ett gitter kan ha två eller tre dimensioner. Gitterpunkterna i ett tredimensionellt oändligt gitter kan definieras av tre translationsvektorer, kalla dessa \vec{a}_1,\vec{a}_2\mbox{ och }\vec{a}_3, så att gittret ter sig likadant om betraktat från punkten \vec{r} som om betraktat från punkten \vec{r}^{\mbox{ }\prime}=\vec{r}+u_1\vec{a}_1+u_2\vec{a}_2+u_3\vec{a}_3 där u1,u2,u3 är godtyckliga heltal. 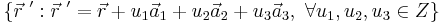\{ \vec{r}^{\mbox{ }\prime}:\vec{r}^{\mbox{ }\prime}=\vec{r}+u_1\vec{a}_1+u_2\vec{a}_2+u_3\vec{a}_3,\mbox{ } \forall u_1,u_2,u_3 \in Z\} definierar gittret.

I två dimensioner kan ett gitter ha fem olika Bravaisgitter: fyrkant, hexagonal, rektangulär, centrerat rektangulär och skev, och det finns sjutton symmetrigrupper i planet. I tre dimensioner finns det fjorton Bravaisgitter, som är baser för alla kristallstrukturer.


E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.

Externa länkar

Hämtad från "https://sv.rilpedia.org/wiki/Gitter_(grupp)"
Personliga verktyg