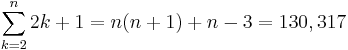Geoid
Från Rilpedia
En geoid (av grekiska: geo, jord och eides, liknande) är en ekvipotentiell yta (ytan som motsvarar ett specifikt värde) som ungefär sammanfaller med havsytans genomsnittliga nivå. Den sägs ofta vara en nära återgivning eller fysisk modell av jordens äkta form och enligt Carl Friedrich Gauss är geoiden en "matematisk bild av jorden" eller, egentligen, av dess gravitationsfält.
Geoidens yta är mer oregelbunden än den rotationsellipsoid som ofta används för att ungefärligen beskriva den fysiska jordens form, men betydligt jämnare än jordens fysiska yta. Medan den senare har toppar på över 8 000 meter (Mount Everest) och dalar på under 11 000 meter (Marianergraven) varierar geoiden enbart med omkring ±100 m från en noggrant fastställd rotationsellipsoid.
En konsekvens av att geoiden är en ekvipotentiell yta är att tyngdkraften är vinkelrät mot geoiden i varje punkt. Detta gör att havsytan skulle anta en form som sammanfaller med geoiden om havsvattnet fick verka fritt, oberoende av andra krafter och kontinenternas landmassor. Geodeter kan beräkna höjden hos punkter på kontinenterna ovanför denna tänkta men fysiskt definierade yta genom en teknik som kallas avvägning.
Till sjöss kan inte undulationerna (avvikelserna) hos geoiden iakttas - en lokal vertikal är alltid rätvinklig och en lokal horisont är alltid tangentiell mot den. En GPS-mottagare ombord skulle dock kunna visa höjdvariationerna relativt mot den (matematiskt definierade) referensellipsoiden vars centrum sammanfaller med jordens masscentrum, och också utgör origo i de koordinatsystem som används inom GPS-systemet.
Harmoniska sfäravbildningar
För att approximera geoidens form är en typ av matematiska funktioner, så kallade klotytefunktioner, särskilt väl lämpade. En av de bästa av sådana modeller är för närvarande EGM96 (Earth Gravity Model 1996) som fastställdes vid ett internationellt samarbetsprojekt som leddes av NIMA. Den ger en komplett utveckling av den globala geoiden i klotytefunktioner ner till detaljer så små som 55 km.
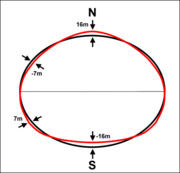
Den matematiska beskrivningen av denna modell lyder:
där
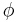 och
och 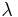 är den geocentriska (sfäriska) latituden och longituden,
är den geocentriska (sfäriska) latituden och longituden,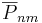 är den fullt normaliserade Legendrefunktionen av grad
är den fullt normaliserade Legendrefunktionen av grad 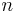 och ordning
och ordning 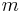 och
och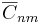 och
och 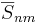 är modellens koefficienter.
är modellens koefficienter.
Den ovanstående formeln ger Jordens gravitionella potential 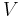 vid positionen
vid positionen 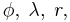 där koordinaten
där koordinaten 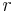 är den geocentriska radien, det vill säga avståndet från jordens centrum. Gradient hos denna potential ger även en modell av den gravitionella accelerationen. Man kan visa att där finns
är den geocentriska radien, det vill säga avståndet från jordens centrum. Gradient hos denna potential ger även en modell av den gravitionella accelerationen. Man kan visa att där finns
olika koefficienter (inklusive både 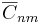 och
och  ). För många användningsområden är den kompletta serien onödigt komplex och trunkteras efter ett fåtal (ungefär efter några dussin) termer.
). För många användningsområden är den kompletta serien onödigt komplex och trunkteras efter ett fåtal (ungefär efter några dussin) termer.
Referenser
- Weikko A. Heiskanen och Helmut Moritz, "Physical Geodesy", W. H. Freeman and Company, 1967
Externa länkar
(engelska)NGAs (f.d. NIMAs) huvudsida om Jordens gravitationsmodeller
(engelska)NASA GSFC Earth gravity page
(engelska)NOAAs geoidhemsida
(engelska)Geoidhandbok av Li och Gotze (PDF)




![V=\frac{GM}{r}\left(1+{\sum_{n=2}^{360}}\left(\frac{a}{r}\right){\sum_{m=0}^n}
\overline{P}_{nm}(\sin\phi)\left[\overline{C}_{nm}\cos m\lambda+\overline{S}_{nm}\sin m\lambda\right]\right),](/w/images/sv.rilpedia.org/math/8/0/1/8011bbcc42aff8615fe8b583e5815fa2.png)