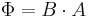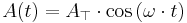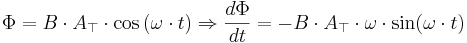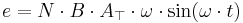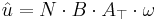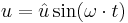Generatorprincipen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Generatorprincipen är som motorprincipen, fast omvänd.

När en elektrisk ledare vrids runt i ett magnetfält induceras en elektromotorisk spänning i ledaren. Om en yttre belastning ansluts kommer den inducerade spänningen att ge upphov till en ström i kretsen. För varje gång ledaren passerar mittlinjen mellan polerna ändrar spänningen polaritet och strömmen sin riktning.


En funktion för den genererade växelspänningen kan lösas ut. Det magnetiska flödet i ledaren

\Phi = B \cdot A

A är arean som ledaren täcker, B är flödestätheten. När det magnetiska flödet genom ledaren ändras induceras en spänning i den. När ledaren roterar förändras det magnetiska flödet genom ledarens area.

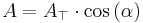A = A_{\top} \cdot \cos{(\alpha)}.

Där Atop är maxarean, alltså när ledaren ligger platt mot magnetfältet och α = 0. Arean förändras enligt funktionen

A(t) = A_{\top} \cdot \cos{(\omega \cdot t)}

där ω är vinkelhastigheten. Den inducerade spänningen är

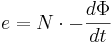e = N \cdot -\frac{d\Phi}{dt}.

Om vi sätter in funktionen för A (Arean) i formeln för Φ får vi

\Phi = B \cdot A_{\top} \cdot \cos{(\omega \cdot t)} \Rightarrow \frac{d\Phi}{dt} = - B \cdot A_{\top} \cdot \omega \cdot \sin(\omega \cdot t)
e = N \cdot B \cdot A_{\top} \cdot \omega \cdot \sin(\omega \cdot t)


Vi kan teckna konstanten û och få en enklare funktion för den genererade växelspänningen

\hat{u} = N \cdot B \cdot A_{\top} \cdot \omega
u = \hat{u} \sin(\omega \cdot t)
Nuvola apps energy.png Denna elektricitetsrelaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Generatorprincipen"
Personliga verktyg