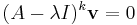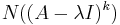Generaliserad egenvektor

Texten från svenska Wikipedia

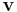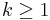Inom linjär algebra är en generaliserad egenvektor $\mathbf{v}$ till en matris $A$ en vektor som hör till ett egenvärde $λ$ med algebraisk multiplicitet $k \geq 1$ .

$(A-\lambda I)^k\mathbf{v} = 0 \,$

För $k = 1$ är 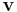$\mathbf{v}$ en vanlig egenvektor.

Man kan också definiera ett generaliserat egenrum till $A$ och ett egenvärde $λ$ med algebraisk multiplicitet 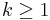$k \geq 1$ som:

$N((A-\lambda I)^k) \,$

Där $N$ står för nollrummet.

Generaliserade egenrum används vid framtagning av Jordans normalform.

Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.