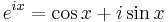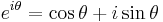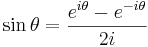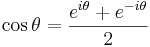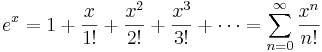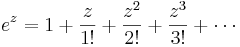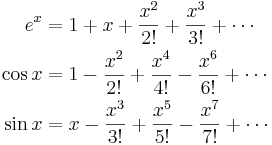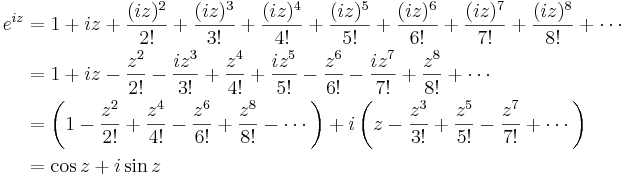Eulers formel
Från Rilpedia
- Se Eulers formel (geometri) för det resultat gällande konvexa polyedrar som även kallas "Eulers formel"

Eulers formel inom komplex analys, uppkallad efter Leonhard Euler, kan tecknas
Den kopplar således samman exponentialfunktionen och de trigonometriska funktionerna.
En enkel konsekvens av Eulers formel är Eulers identitet
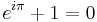 ,
,
en formel som förbluffat matematikstudenter genom tiderna. Formeln relaterar tre tal från helt olika delar av matematiken: talet 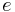 från analysen, talet
från analysen, talet 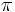 från geometrin, den komplexa enheten/talet
från geometrin, den komplexa enheten/talet 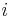 och talet
och talet 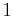 från aritmetiken. Formeln kopplar som synes samman flera delar av matematiken.
från aritmetiken. Formeln kopplar som synes samman flera delar av matematiken.
Formeln kan härledas ur Taylorutvecklingen av 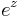 genom att sätta
genom att sätta 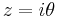 . Det finns även en omvänd variant som kallas Eulers formler, vilka istället uttrycker de trigonometriska funktionerna sinus och cosinus med hjälp av exponentialfunktionen:
. Det finns även en omvänd variant som kallas Eulers formler, vilka istället uttrycker de trigonometriska funktionerna sinus och cosinus med hjälp av exponentialfunktionen:
Bevis av Eulers formel
Taylorserien för den reella exponentialfunktionen 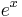 kan skrivas
kan skrivas
Detta motiverar definitionen av den komplexa exponentialfunktionen enligt
Funktionerna 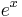 ,
, 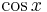 och
och 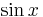 (där
(där 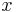 är ett reellt tal) kan taylorutvecklas runt noll, vilket ger följande serier:
är ett reellt tal) kan taylorutvecklas runt noll, vilket ger följande serier:
För komplexa tal 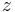 , definieras var och en av dessa funktioner av respektive serie genom att
, definieras var och en av dessa funktioner av respektive serie genom att 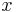 ersätts med
ersätts med 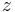 (där
(där 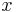 är ett reellt och
är ett reellt och 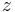 är ett komplext tal). Detta är tillåtet om högerleden existerar för alla
är ett komplext tal). Detta är tillåtet om högerleden existerar för alla 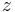 , vilket är fallet då konvergensradierna är oändliga. De tre serierna är absolutkonvergenta för alla
, vilket är fallet då konvergensradierna är oändliga. De tre serierna är absolutkonvergenta för alla 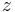 . Då gäller:
. Då gäller:
Notera att om 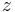 sätts till ett reellt tal
sätts till ett reellt tal 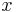 så erhålls Eulers formel på den form vi är vana att se den:
så erhålls Eulers formel på den form vi är vana att se den: