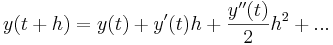Eulers stegmetod
Från Rilpedia
Eulers stegmetod (en. Euler's method), numerisk analys, numerisk metod för att lösa differentialekvationen y' = f(t, y) genom att dela in den i diskreta stegintervall. Metoden utgår från Taylorserien
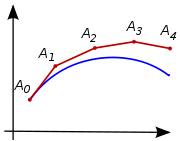
där man försummar termer av högre ordning än två. Man approximerar alltså funktionens lösningskurva med sin tangent i varje punkt och beräknar nästa punkt på kurvan genom att följa tangentens riktning.
Eftersom y' = f(t, y) fås
- y(t + h) = y(t) + f(t,y(t))h
eller i diskret form
- yk + 1 = yk + f(tk,yk)hk
Tidsstegen ges av tk och tk + 1 = tk + hk och steglängen hk väljs på sådant sätt att största noggrannhet erhålls, vilket kan bli ett större problem än grundproblemet. Ofta väljs hk = h, där h är en konstant.
Eulers stegmetod är en s.k. enstegsmetod eftersom den bara baserar sig på information från steget före. Noggrannheten är exakt för homogena differentialekvationer av första ordningen. Stabiliteten varierar beroende på differentialekvation; i vissa fall växer felet exponentiellt, medan i andra fall avtar felet exponentiellt.
Innehåll |
Felanalys
För (globala) trunkeringsfelet i Eulers stegmetod gäller
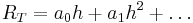 .
.
Exempel
Låt y ′ = 3t — y, y 0 = 2, steglängden h = 0,5.
Det vill säga vi startar i punkten (0, 2). I denna punkt beräknar vi lösningskurvans lutning:
y ′ (0) = 3*0 — 2 = -2
Med steglängden 0,5 blir nästa t-värde 0 + 0,5 och nästa y-värde = 2 + (-2)*0,5 = 1. Så håller vi på och stegar oss framåt tills vi når det t-värde vi är intresserade av.
Följande tabell visar de beräknade värdena som ger en numerisk uppskattning av y (2) :
| t | y (t ) | y ′(t ) |
|---|---|---|
| 0 | 2 | –2 |
| 0,5 | 1 | 0,5 |
| 1 | 1,25 | 1,75 |
| 1,5 | 3,25 | 2,125 |
| 2 | 2,75 |
Alltså är y(2) = 2,75 enligt Eulers stegmetod, med steglängden 0,5 Om ett mindre h hade använts, så hade man fått fram ett mycket noggrannare värde.
Detta svar kan jämföras med den exakta lösningen som är y(t ) = 5e-t + 3t - 3 och som då ger att y(2) = 5e-2 + 3 = 3,68. Att det blev så stor skillnad är inte att förvånas över, för att få ett någorlunda bra svar bör h vara som mest en tiondel av intervallet, d.v.s. ungefär 0,1 eller 0,2 i det här fallet.
Se även
- Taylorseriemetod
- Heuns metod
- Mittpunktsmetoden
- Runge-Kuttas metod
- Extrapoleringsmetod
- Flerstegsmetod
- Flervärdesmetod
Externa länkar
Referenser
- Michael T. Heath, Scientific Computing - an introduction survey, McGraw-Hill (1997)