Elastiska linjens ekvation

Texten från svenska Wikipedia

Den elastiska linjens differentialekvation beskriver momentet i en balk vid balkböjning och tecknas:

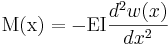
$\mathrm{M(x)} = \mathrm{-EI} \frac{d^2w(x)}{dx^2}$

där $M$ är böjmomentet, $E$ är elasticitetsmodulen, $I$ är balktvärsnittets yttröghetsmoment och 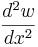$\frac{d^2w}{dx^2}$ är utböjningens andraderivata. Produkten 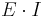$E \cdot I$ brukar även kallas balkens böjstyvhet.

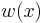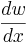Elastiska linjen används för att bestämma balkens utböjning, $\textstyle w(x)$ eller balkens lutningsvinkel $\frac{dw}{dx}$ .

Elastiska linjens differentialekvation kan kombineras med andra ekvationer eller samband. Exempel:

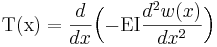
$\mathrm{T(x)} = \frac{d}{dx}\Big(\mathrm{-EI} \frac{d^2w(x)}{dx^2}\Big)$

där $T$ är tvärkraften

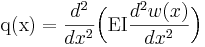
$\mathrm{q(x)} = \frac{d^2}{dx^2}\Big(\mathrm{EI} \frac{d^2w(x)}{dx^2}\Big)$

där $q$ är lastintensiteten och beror av utbredd last per längdenhet $Q / L$ . Vanligt är att $q$ skrivs $q = - Q / L$

Denna mekanikartikel är bara påbörjad. Du kan hjälpa till genom att utöka den.