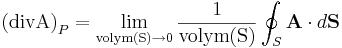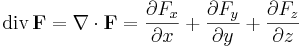Divergens (vektoranalys)
Från Rilpedia
Denna artikel avser ett specifikt begrepp inom vektoranalys. För andra betydelser av termen, även inom matematik, se Divergens.
I vektoranalys är divergens ett mått på ett vektorfälts tendens att "stråla" ut från (eller konvergera in mot) en viss punkt. Divergensen själv är ett skalärfält och definierad som en funktion av vektorfältet.
Som exempel kan vektorfältet vara hastigheten för molekylerna i en gas som expanderar när den upphettas. För ett sådant vektorfält har divergensen ett positivt värde, eftersom gasen expanderar (överallt). Om gasen däremot kyls så drar den ihop sig, och divergensen blir negativ.
Divergensen för ett vektorfält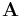 
i en punkt P kan definieras som ett gränsvärde för en ytintegral som omsluter punkten, så här:
där volym(S) betecknar mätetalet för den volym som den slutna ytan S omsluter.
Benämningen divergens är väl vald. Man kan säga att divergensen mäter hur mycket något flödar ut (divergerar) från en sluten kropp, till exempel en boll (även andra former är tillåtna, som till exempel en kub eller cylinder, bara den är tillräckligt liten). Som en bildlig liknelse kan man tänka sig en liten boll ur vilken vatten sprutar ut åt alla håll. I vissa riktningar sprutar det mindre, och i andra mer. Divergensen anger hur mycket vatten som sprutar ut ur den lilla bollen totalt. Är divergensen noll så sprutar inget vatten ut ur bollen även om vattnet inne i bollen mycket väl kan "virvla omkring", se även rotation (alternativt flödar det in lika mycket vatten i bollen som det sprutar ut, så att den totala mängden vatten i bollen förblir konstant)
I ett kartesiskt koordinatsystem ges divergensen av
och denna relation kan också användas som definition. Det är speciellt lämpligt att använda uttrycket ovan för att praktiskt beräkna ett vektorfälts divergens.
Ett vektorfält vars divergens är 0 (som dock är definierat) i hela området sägs vara solenoidalt eller källfritt. Ett exempel på ett sådant vektorfält är det magnetiska B-fältet inom elektrodynamiken.
