Från Rilpedia

Dijkstras algoritm är en matematisk algoritm för att hitta den billigaste vägen från en given nod till alla andra noder i en viktad och riktad graf med positiva bågkostnader. Algoritmen har fått sitt namn efter Edsger Dijkstra, som upptäckte den år 1959. Den är en girig algoritm som systematiskt löser Bellmans ekvationer, som utgör optimalitetsvillkoren för ett billigast väg-problem:

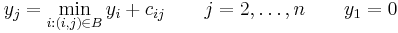
Lösningar till problemet med den billigaste vägen behövs inom många områden, exempelvis inom routing för att hitta den kortaste vägen när transportsträckor läggs ut.

Innehåll 1 Algoritmbeskrivning 2 Exempel 3 Varianter 4 Bevis 5 Komplexitet 6 Implementering 7 Källa

Algoritmbeskrivning

Beskrivningen nedan löser problemet att finna den billigaste vägen från startnoden n_s till terminalnoden n_t där c_ij beskriver kostnaden på bågen 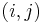. Låt y_i representera den kortaste vägen till nod i och p_i dess föregångare.

1. Sätt y_s = 0. För alla andra noder, sätt .
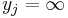2. Finn den nod i med lägst nodpris y_i som ännu inte är avsökt.
3. Undersök varje båge 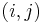som utgår från nod i. Om den representerar en billigare väg till nod j, det vill säga att y_i + c_ij < y_j, uppdateras värdena för nod j med y_j = y_i + c_ij och p_j = i.
4. Gå till steg 2 om inte alla noder är avsökta.

När algoritmen är färdig återfinns den billigaste vägen genom att avläsa föregångaren p_t till slutnoden, sedan den nodens föregångare, och så vidare.

Exempel

Bilden visar ett exempel av Dijkstras algoritm, där de olika variablernas värden visas under körning. Den optimala vägen från nod a till nod b beräknas. Initialt sätts nodpriserna till 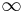för alla noder utom startnoden, som får nodpris 0. För varje nod beräknas de närliggande nodpriserna, och noden markeras därefter som avsökt genom den röda fyllningen.

När slutnoden b avsöks har den optimala vägen beräknats.

Varianter

Dijkstras algoritm löser inte garanterat problemet när vissa bågkostnader är negativa. Bellman-Fords algoritm löser detta genom att i steg 3 markera nod j som icke avsökt. Med icke-negativa bågkostnader är j redan icke avsökt.

Bevis

Efter att nod i i algoritmbeskrivningen markerats som avsökt har alla avsökta noder fått permanenta nodpriser, som representerar priset av den billigaste från startnoden dit. Varje ännu ej avsökt nod har ett nodpris, som är priset på den billigaste vägen från startnoden dit genom de redan avsökta noderna. Denna egenskap behålls i varje iteration av algoritmen. När alla noder är markerade som avsökta är alltså även varje nodpris det optimala.

Att egenskapen behålls i varje iteration kan bevisas genom att antaga att den nod i som väljs att avsöka har nodpriset y_i som inte är optimalt. Då skulle det finnas en väg genom de ej avsökta noderna som är billigare. Kalla en av dessa noder för nod k. Eftersom alla bågar i grafen är positiva (annars är Dijkstras algoritm inte applicerbar) måste priset för billigaste vägen från nod k till nod i vara positiv. Billigaste vägen från startnoden till nod k är nodpriset y_k. Det betyder att vägen från startnoden till nod i är dyrare än vägen till nod k.

Från metoden med vilken vi valde nod i ser vi dock att nodpriset y_i inte är lägre än nodpriset y_k. Där ligger en motsägelse. Alltså var det ursprungliga antagandet felaktigt, och nodpriset y_i är optimalt.

Komplexitet

Om man implementerar prioritetskön med hjälp av en Fibonacci heap så har algoritmen tidskomplexiteten 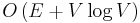, där V är antalet noder och E är antalet vägar i grafen.

Implementering

Följande program är en implementering av Dijkstras algoritm i pseudokod.

   DIJKSTRA (Graf G, startnod s)
       // Vi initierar alla noder i grafen.
       // Billigaste vägen (avståndet) är oändligt
       //  och föregående nod är odefinierad
       för i ∈ Noder(G) gör
           avstånd[i] = OÄNDLIGT
           föregångare[i] = NULL
       // Avståndet till startnoden är 0
       avstånd[s] = 0
       //markera startnoden som avsökt
       Avsökt( s )
       medan inte alla noder avsökta gör
           // Finn den ej avsökta nod som har lägst nodpris
           //  tills alla är avsökta
           i = Minimum( ej avsökta noder )
           för j ∈ närliggande(i) gör
               // Undersök om det finns en billigare väg
               //  via nod i till närliggande noder
               om avstånd[j] > avstånd[i] + kostnad(i, j) gör
                   avstånd[j] = avstånd[i] + kostnad(i, j)
                   föregångare[j] = i
           Avsökt( i )

Källa

• Jan Lundgren, Mikael Rönnqvist och Peter Värbrand. Optimeringslära, upplaga 3:1. Studentlitteratur 2003. ISBN 978-91-44-05314-1.