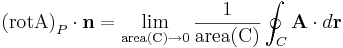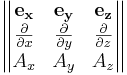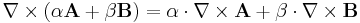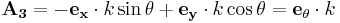Rotation (vektoranalys)

Från Rilpedia

(Omdirigerad från Curl)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Rotation (rot eller curl) är en operator inom vektoranalys. Ett vektorfälts rotation i en punkt $P$ är en vektor. Denna vektors komponent längs en axel 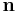$\mathbf{n}$ kan definieras som gränsvärdet för en cirkulationsintegral enligt formeln:

$\left(\mathrm{rot A}\right)_{P} \cdot \mathbf{n} = \lim_{\textrm{area(C)} \rightarrow 0} \frac{1}{\textrm{area(C)}} \oint_{C} \mathbf{A} \cdot d\mathbf{r}$

där $area(C)$ betecknar mätetalet för den area som omsluts av den slutna kurvan $C$ , där $C$ innehåller $P$ och är i ett plan vinkelrätt mot 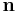$\mathbf{n}$ . Fysikaliskt betyder alltså rotationen att vi mäter arbetet (räknat med tecken) som går åt för att flytta en liten partikeln runt en punkt $P$ med axeln i riktning 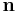$\mathbf{n}$ i till exempel cirkulära små banor (det går även bra med andra former på banorna, säg fyrkantiga eller elliptiska).

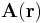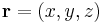I kartesiska koordinater kan rotationen till ett vektorfält $\mathbf{A}(\mathbf{r})$ , där $\mathbf{r} = (x,y,z)$ betecknar ortsvektorn, beräknas genom att man bestämmer den formella determinanten

$\left\| \begin{matrix} \mathbf{e_x} & \mathbf{e_y} & \mathbf{e_z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ A_x & A_y & A_z \\ \end{matrix} \right\|$

där till exempel $A x$ avser x-koordinaten av vektorfältet $A$ och inte derivering m.a.p. x eller liknande.

Formellt kan man skriva rotationen som en differentialoperator så här: 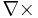$\nabla \times$ .

Man är intresserad av rotationen därför den ger en (första) generalisering av analysens fundamentalsats, d.v.s. hur en ytintegral ges i form av en integral längs ytans rand. Istället för att obestämd integral och derivata är inversa operationer, blir rotationen och ytintegration inversa par, på analogt (men ej exakt samma) sätt. Motsvarande (andra) generaliseringar ges av begreppet divergens. Rotation och divergens är alltså nära sammankopplade; de övergår f.ö. båda i Greens formel i planet när man betraktar vektorfält bara i planet.

Man kan visa att rotationen i en punkt mäter hur mycket ett mycket litet "paddelhjul" snurrar i punkten, närmare bestämt är den dubbla vinkelhastigheten. Skulle man jämnt fördelat strö ut barr i en vattenvirvel, säg, när man tappar ur vattnet ur badkaret borde de ge en bra bild av hur rotationen som uppstår av vektorfältet (som härrör från kraften badkarsutsuget ger upphov till) geometriskt ser ut i varje punkt. Man inser att benämningen rotation är väl vald.

Ett vektorfält vars rotation är noll kallas virvelfritt, vilket känns naturligt i ljuset av ovanstående geometriska beskrivning.

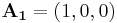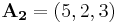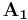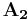Typiska virvelfria vektorfält inkluderar alla konstanta funktioner som till exempel $\mathbf{A_{1}} = \left(1,0,0\right)$ och $\mathbf{A_{2}} = \left(5,2,3\right)$ (hur mycket skulle barr rotera om man släppte ner dem? Inte alls, de skulle bara flyta med i riktningen som ges av vektorn $\mathbf{A_1}$ eller $\mathbf{A_2}$ !). Mindre trivialt är att även ortsvektorn 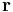$\mathbf{r}$ är virvelfri. Att den är virvelfri i origo är intuitivt, men inte helt intuitivt att den verkligen är det även bortanför origo, säg när man translaterat den längs en vektor 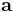$\mathbf{a}$ . Att den verklingen är virvelfri även utanför centrum inses nog lättast genom att man begrundar faktumet vektoroperatorn 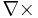$\nabla \times$ är linjär, d.v.s. för godtyckliga reella konstanter $α$ och $β$ gäller

$\nabla \times \left( \alpha \mathbf{A} + \beta \mathbf{B} \right) = \alpha \cdot \nabla \times \mathbf{A} + \beta \cdot \nabla \times \mathbf{B}$

Ett enkelt icke-virvelfritt fält, å andra sidan, och som "virvlar" lika mycket överallt (har konstant norm, oberoende av mätpunkt) ges av

$\mathbf{A_3} = -\mathbf{e_x} \cdot k \sin \theta + \mathbf{e_y} \cdot k \cos \theta = \mathbf{e_{\theta}} \cdot k$

Det har styrka $k$ och snurrar med axel i riktningen 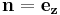$\mathbf{n} = \mathbf{e_z}$ (ett badkar ger nog inte en virvel av sådan typ - troligen roterar virveln snabbare närmare utsuget). Eftersom dubbla vinkelhastigheten ger rotationen, får man vinkelhastigheten av detta uttryck:

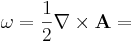$\mathbf{\omega} = \frac{1}{2} \nabla \times \mathbf{A} =$ beräkna den formella determinanten ovan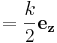 $= \frac{k}{2} \mathbf{e_z}$

Farten ges alltså av halva styrke-konstanten.

Som följd av Helmholtz teorem är vektorfältet bestämt av dess rotationsdel och dess divergensdel (under någon förutsättning). Vet man båda dessa, löst uttryckt, "generaliserade derivatorna" vet man också funktionen.

Rotation (vektoranalys)

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk