Binärt sökträd

Från Rilpedia

Texten från svenska Wikipedia

Ett binärt sökträd av storlek 9 och höjd 3. Rotvärdet är 8 och löven är 1, 4, 7 och 13

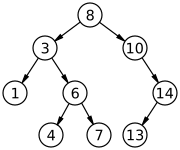
Ett binärt sökträd är ett binärträd (dvs varje nod har högst två barn) med följande egenskaper:

• varje nod har ett värde.
• det högra delträdet till en nod innehåller bara värden som är högre än värdet i noden.
• det vänstra delträdet till en nod innehåller bara värden som är lägre än värdet i noden.

Binära sökträd är användbara eftersom det finns effektiva sökalgoritmer som kan användas på dem. I genomsnitt är algoritmen av ordning Θ(log n) och i värsta fall Θ(n).

Operationer

Alla de olika operationer man kan göra på ett binärt sökträd använder sig av en jämförelseoperator, som definieras som en funktion som tar in två parametrar och bestämmer ordningen på dessa två. I nedanstående algoritmer så använder vi tecknen < och > för att beteckna mindre eller större än.

Sökning

Att söka i ett binärt sökträd kan göras effektivt då trädet byggts upp för att klara av just detta. Vi börjar med att undersöka rotnoden och har då tre alternativ: värdet är större än noden och vi hittar då värdet i det högra delträdet, värdet är mindre än noden och vi hittar då värdet i det vänstra delträdet eller så är värdet lika med noden och vi har då hittat vårt svar. Efter denna jämförelse går vi till nästa nod (antingen åt höger eller vänster) och gör samma jämförelse där. Vi upprepar detta tills vi hittat vårt värde.

Operationen har komplexiteten O(n) och i värsta fall, med ett obalanserat träd där alla högra eller vänstra delträd är tomma (ett degenererat träd med samma egenskaper som en länkad lista), är komplexiteten O(n^2).

Ett exempel i programspråket Python:

 def search_binary_tree(node, key):
     if node is None:
         return None  # nyckeln återfanns inte
     if key < node.key:
         return search_binary_tree(node.left, key)
     else if key > node.key:
         return search_binary_tree(node.right, key)
     else:  # nyckeln har samma värde som nodens värde
         return node.value  # hittat nyckel!

Traversering

Att genomsöka alla noderna i ett träd kallas att traversera trädet. Detta kan göras genom post-, pre- eller inordertraversering.

Om inordertraversering appliceras på ett binärt sökträd fås elementen i växande ordning.

Insättning

Tack vare det binära trädets uppbyggnad är det lätt att göra en insättning. Insättning görs vid den första lediga lövnoden. Efter insättning görs vanligvis en sortering av trädet så att eventuella rotationer för att balansera trädet kan utföras.

Borttagning

Detta korta avsnitt behöver utökas.

Sortering

Detta korta avsnitt behöver utökas.

Typer av binära sökträd

Detta korta avsnitt behöver utökas.

 Denna datatekniksrelaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.