Asymptot
Från Rilpedia
Inom matematiken är en asymptot en rät linje (eller annan enkel kurva) som en funktion närmar sig allt mer när man närmar sig definitionsmängdens gränser. Huvudsakliga användningsområdet är att approximera hur en funktion uppför sig i något område (vanligen då variabeln är mycket stor, det vill säga går mot oändligheten).
Innehåll |
Lodrät asymptot
Uppträder då funktionen har en pol i en punkt. Exempel inkluderar f(x) = 1 / (x 2 - 1), som har en lodrät asymptot i x = 1 och en i x = - 1. f(x) = (x 3 - 1) / (x 2 - 1) har bara en lodrät asymptot i x = - 1 då gränsvärdet för f(x) då x går mot - 1 från vänster och höger är oändligheten. Denna funktion har ingen asymptot i x = 1 för att dess gränsvärde är 0/0 då x går mot 1.
Vågrät asymptot
Om funktionen f(x) har ett gränsvärde a då x går mot plus (minus) oändligheten, så är y = a en vågrät linje och en vågrät asymptot till f.
Sned asymptot
För vissa funktioner gäller att f(x) beter sig ungefär som en linjär funktion då x går mot oändligheten. Denna linjära funktion kallas för en sned asymptot. Enklast beräknas den genom att ansätta den linjära funktionen som ax+b, och lösa ekvationen
för konstanterna a och b.
Asymptotiska kurvor
För att beskriva en funktions beteende för stora värden på variabeln, räcker det ibland inte med raka asymptoter. I likhet med fallet 'sned asymptot' säger man att en given kurva y = g(x) är asymptotisk till funktionen f(x) om
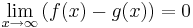 .
.
Exempelvis har f(x) = x2(1 - 1 / x3) + e-x en asymptotisk kurva i form av y = x2, då x går mot positiva oändligheten.