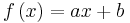Affin avbildning
Från Rilpedia
En affin avbildning (även kallad affin transformation eller affin funktion) är inom matematik en sammansättning av en linjär avbildning och en translation. Geometriskt utgör de affina avbildningarna alla operationer som bevarar räta linjer.
Ett grundläggande exempel utgörs av förstagradspolynomen, på formen
Om b =0, så har vi specialfallet homoteti, som i sin tur är ett specialfall av linjära avbildningar. (Det faktum att grafen alltid är en linje gör alltså inte att villkoren för linearitet uppfylls annat än när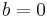 
.)
För en vektor x i det n-dimensionella euklidiska rummet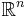 
kan en affin avbildning y uttryckas på formen
- y(x) = Ax + b
där A är n×n-matrisen för en linjär avbildning och b är en translationsvektor. Även sammansättningen av två affina avbildningar är en affin avbildning, eftersom
- C(Ax + b) + d = (CA)x + (Cb + d)
har samma form.
Genom att lägga till en virtuell dimension kan en affin avbildning utföras genom enbart en matrismultiplikation. Detta utnyttjas ofta i datorsystem, till exempel i OpenGL och Postscript.
