Från Rilpedia

De fyra Ackermanntalen är: 1↑1, 2↑↑2, 3↑↑↑3 och 4↑↑↑↑4. Notationen med pilar infördes 1976 av Donald Knuth men funtionen definierades av Wilhelm Ackermann 1926. I denna artikel används Knuths pilnotation för att kunna beskriva de större talen.

Storleken på Ackermanntalen

Det första Ackermanntalet är alltså 1 och det andra Ackermanntalet är:

2² = 4

Det tredje Ackermanntalet är:

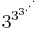
Där antalet treor är:

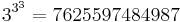
Det fjärde Ackermanntalet är ofattbart stort. 4↑↑↑↑4 är detsamma som 4↑↑↑4↑↑↑4↑↑↑4↑↑↑4 som är detsamma som:

4↑↑4↑↑4...↑↑4↑↑4↑↑4,

där antalet fyror är

4↑↑4↑↑4...↑↑4↑↑4↑↑4,

och här är antalet fyror:

4↑↑4↑↑4↑↑4↑↑4

Detta sista tal är

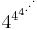
där antalet fyror är

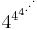
där antalet fyror är

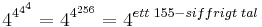
Källa: Boken om tal av John Conway och Richard K Guy.