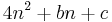Ulams spiral
Från Rilpedia
Ulams spiral är en uppställning av primtalen, de heltal som inte är delbara med något annat tal förutom 1, som uppvisar märkliga mönster. Den upptäcktes år 1963 av matematikern Stanislaw Ulam, då han uttråkad försökte fördriva tiden under ett vetenskapligt möte med hjälp av en penna och ett rutat papper. Han skrev ner talen 1, 2, 3, ... i en spiral och markerade primtalen:
37--36--35--34--33--32--31 37-- -- -- -- -- --31 | | | | 38 17--16--15--14--13 30 17-- -- -- --13 | | | | | | | | 39 18 5-- 4-- 3 12 29 5-- -- 3 29 | | | | | | | | | | | | 40 19 6 1-- 2 11 28 19 -- 2 11 | | | | | | | | | | 41 20 7-- 8-- 9--10 27 41 7-- -- -- | | | | | | 42 21--22--23--24--25--26 -- --23-- -- -- | | 43--44--45--46--47--48--49... 43-- -- -- --47-- -- ...
Till sin förvåning lade Ulam märke till att primtalen tycks hamna längs diagonala linjer. Det visar sig att liknande mönster upprepas då spiralen görs mycket större (se bild), samt att primtalen faller längs diagonaler även då något annat tal än 1 väljs som utgångspunkt.
En konsekvens är att det tycks finnas många konstanter b och c sådana att polynomet
ger upphov till oväntat många primtal. Mönstren i Ulamspiralen har dock aldrig förklarats till fullo, och är intressanta med tanke på att primtalen i många avseenden tycks vara "slumpmässigt" utspridda bland heltalen. Upptäckten sågs som så betydelsefull att Ulams spiral år 1964 hamnade på omslaget till Scientific American.