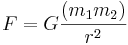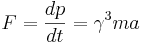Tröghet
Från Rilpedia
- För andra betydelser, se Tröghet (olika betydelser).
Tröghet definieras inom fysiken som motstånd mot rörelseförändring. Begreppets innebörd har utvecklats i takt med naturvetenskapens landvinningar, men dess orsaker är fortfarande okända.
Tröghet är en kortform för "tröghetsprincipen" som den beskrevs av Isaac Newton i hans första rörelselag. I vanligt språkbruk används termen "tröghet" också för att kvalitativt hänvisa till ett föremåls "benägenhet att motstå hastighetsändringar", vilket bestäms av dess massa.
Innehåll |
Historik och begreppets framväxt
Antika och medeltida uppfattningar
Antikens filosofer intresserade sig tidigt för rörelse. Redan på 400-talet före vår tideräkning ville Zenon från Elea med sina paradoxer visa att rörelse var omöjlig. Begreppet tröghet var dock inte påtänkt och det blir en modern övertolkning att skylla den för orsak.
Till Aristoteles kärnpunkter hör hans rörelselära[1], som är kopplad till kosmologin och definierar tre huvudtyper av rörelse:
- Naturlig rörelse, a. nedåtriktad mot universums centrum, b. uppåtriktad mot universums periferi eller c. cirkulär
- Påtvingad rörelse, som den kastade stenens
- Frivillig avsiktlig rörelse, som endast gäller för levande varelser
Till detta är de fem elementen jord, luft, eld, vatten och kvintessensen kopplade. Tyngd och lätthet såg Aristoteles som uttryck för elementens vilja att återförena sig med den region där de hörde hemma. Elementen strävar alltså efter att uppnå ett viloläge, när de satts i rörelse. Vila blir enligt Aristoteles det naturliga tillståndet för all materia på jorden. Denna elementens vilja fick gälla för tröghet i nästan 2000 år.
Tröghet inom klassisk mekanik
Tröghetsprincipen är ett grundläggande begrepp inom dynamiken, den gren inom mekaniken, som används för att beskriva materiens rörelse och hur den påverkas av krafter:
Varje kropp i ett isolerat system förblir i sitt tillstånd av vila eller konstant rörelse rakt fram, försåvitt den inte tvingas att ändra sin tillvaro av påverkande krafter
I Newtons ekvation
 |
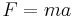(kraft = massa * acceleration) |
definieras m som den tröga massan. Tidigt utfördes experiment för att utröna om den tröga massan var densamma som den tunga massan, där den tunga massan definieras genom
eller
 |
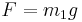med |  . |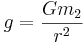
Experimenten kan inte inom felmarginalerna påvisa någon skillnad dessa massor emellan. Detta blev en viktig utgångspunkt för Einstein, när han formulerade sin allmänna relativitetsteori.
Tröghet i relativistisk mekanik och kosmologi
Den matematiska grunden för speciella relativitetsteorin är Lorentztransformationen. Denna är en uppsättning ekvationer som talar om hur tids- och rumskoordinater mäts i olika inertialsystem. Relativitetsteorin utgår från att ljusets hastighet är densamma i alla referenssystem, vilket är tillräckligt för dess härledning. Istället för den klassiska fysikens rörelsemängd,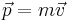 
, visar Einstein att rörelsemängden i själva verket är 
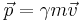, där γ är lorentzfaktorn, som beror på hastigheten 
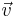. Newtons andra lag med utgångspunkt i tidsvariationen för rörelsemängden gäller även i den speciella relativitetsteorins dynamik och ger då följande uttryck för kraften parallell med rörelseriktningen:
där m fortfarande är den tröga massan. En kraft vinkelrätt mot rörelseriktningen ändrar inte partikelns hastighet, endast dess riktning. Rörelsemångdens tidsderivata är i detta fall γma.
Fastän begreppet massa (och därmed även tröghet) fortfarande är i bruk, så finner man - särskilt på ett heuristiskt plan - att inom allmänna relativitetsteorin de väsentliga fysikaliska uttrycken (de som uppträder i Einsteins fältekvationer) är stressenergitensorn och Riccis krökningstensor, så har i viss mening tröghetsbegreppet överskridits. I stressenergitensorn är det dock möjligt att känna igen termer, som är ett mått på masstäthet och energitäthet.
Se även
Referenser
- ↑ Sinnerstad, U.; Från stjärnskådning till rymdforskning. Lund (1985). ISBN –9157801770
