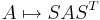Sylvesters tröghetslag
Från Rilpedia
Texten från svenska Wikipedia
Sylvesters tröghetslag (efter J. J. Sylvester, teorem inom linjär algebra som behandlar symmetriska kvadratiska former.
Formulering i termer av matriser
Enligt teoremet så är trögheten hos en symmetrisk matris A invariant under kongruenstransformationer.
Trögheten hos en symmetrisk matris A definieras som tripeln (a,b,c), där a är antalet positiva egenvärden, b är antalet negativa och c är antalet nollvärda egenvärden (räknat med multiplicitet).
Med en kongruenstransformation av A menas här transformationen
där S är en inverterbar matris.
Externa länkar
- Extern länk Sylvester's law från PlanetMath.
