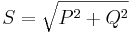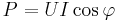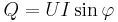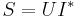Skenbar effekt
Från Rilpedia
Skenbar effekt uppkommer i samband med växelspänningseffekt, då det är otillräckligt att beskriva effekten som produkten av spänning och ström. I växelspänningssystem skiljer man därför på skenbar, aktiv effekt och reaktiv effekt, där den aktiva effekten är den effekt som uträttar nyttigt arbete, exempelvis momentet i en motor eller värme i ett element. Den reaktiva effekten utgör ett mått på den momentana effekt som åtgår på grund av energilagrande komponenter av kapacitiv eller induktiv karaktär. Skenbar effekt är en sammanställning av dessa båda slag av effekt och ger ett mått på den faktiska effekt som en produkt tål eller drar från elnätet.
Effektberäkning
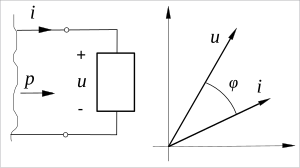
Vi ser av visardiagrammet att den skenbara effekten kan skrivas som
där
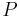 = aktiv effekt [W]
= aktiv effekt [W]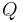 = reaktiv effekt [VAr]
= reaktiv effekt [VAr]
Den aktiva respektive reaktiva effekten beräknas som
där
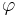 = fasskillnaden mellan ström och spänning
= fasskillnaden mellan ström och spänning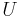 = spänningens effektivvärde
= spänningens effektivvärde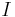 = strömmens effektivvärde
= strömmens effektivvärde
För en given tvåpol och belastningsfall kan effekten vara avgiven eller mottagen beroende på 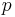 's riktning.
's riktning.
Den skenbara effekten kan också beräknas med hjälp av komplexa tal och kan då skrivas som
Beloppet av 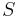 har enheten [VA] (volt-ampere) och är den skenbara effekt som anges som förbrukning för produkter som kopplas till elnätet. Fasen för den skenbara effekten brukar vanligtvis inte anges explicit, utan som en effektfaktor,
har enheten [VA] (volt-ampere) och är den skenbara effekt som anges som förbrukning för produkter som kopplas till elnätet. Fasen för den skenbara effekten brukar vanligtvis inte anges explicit, utan som en effektfaktor, 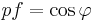 , vilken anger förhållandet mellan skenbar och aktiv effekt.
, vilken anger förhållandet mellan skenbar och aktiv effekt.





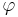 är fasvinkeln mellan spänning och ström. Den reaktiva effektens tecken beror av tecknet för
är fasvinkeln mellan spänning och ström. Den reaktiva effektens tecken beror av tecknet för