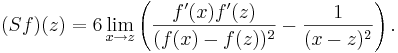Schwarzisk derivata
Från Rilpedia
En Schwarzisk derivata som beskriver hur f ska approximeras av en tangerande möbiusavbildning snarare än av en tangerande linje, som i fallet för vanliga derivator.
Definition
Den Schwarziska derivatan av en funktion 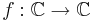 definieras som
definieras som
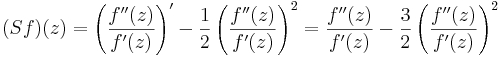 .
.
Alternativt kan den schwarziska derivatan av f definieras som