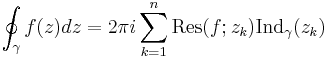Residysatsen
Från Rilpedia
Residysatsen eller Cauchys residysats uttrycker ett samband mellan vissa linjeintegraler av en funktion och dess Laurentserieutvecklingar i funktionens singulära punkter.
Formulering
Antag att f är analytisk innanför och på en enkel sluten kurva γ förutom i ändligt många punkter  , då gäller:
, då gäller:
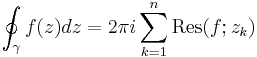 , där integrationsvägen är tagen moturs.
, där integrationsvägen är tagen moturs.
där 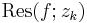 är residyn för f i zk.
är residyn för f i zk.
Ovanstående är ett ofta använt specialfall av en allmänare sats: Låt f vara analytisk i ett område U förutom i ändligt många punkter  och γ vara en sluten kurva (inte nödvändigtvis enkel) som omsluter, men inte går igenom någon av punkterna
och γ vara en sluten kurva (inte nödvändigtvis enkel) som omsluter, men inte går igenom någon av punkterna  . Då gäller:
. Då gäller:
där 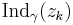 är omloppstalet för kurvan γ kring punkten zk.
är omloppstalet för kurvan γ kring punkten zk.