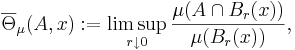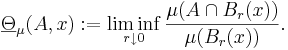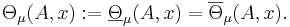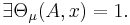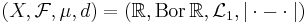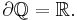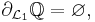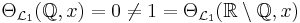Måtteoretisk rand

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Måtteoretiska randen för en mängd A är inom matematik den mängd som innehåller alla punkter som är A:s och A:s komplements tätpunkter.

Innehåll

Tätpunkter

Huvudartikel: Tätpunkt

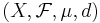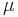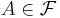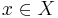Låt (X,\mathcal{F},\mu,d) vara ett metriskt måttrum så att måttet \mu\, är Borel. För A \in \mathcal{F} och x \in X beteckna A:s yttre täthet i x

\overline{\Theta}_\mu (A,x) := \limsup_{r \downarrow 0} \frac{\mu(A \cap B_r(x))}{\mu(B_r(x))},

och A:s innre täthet i x

\underline{\Theta}_\mu (A,x) := \liminf_{r \downarrow 0} \frac{\mu(A \cap B_r(x))}{\mu(B_r(x))}.

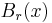där B_r(x)\, är en boll med avseende på metriken d\,.

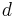Mängden A har en täthet i x om

\Theta_\mu (A,x) := \underline{\Theta}_\mu (A,x) = \overline{\Theta}_\mu (A,x).\,

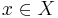En punkt x \in X är en tätpunkt om

\exist\Theta_\mu (A,x) = 1.

Formell definition

Låt 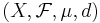(X,\mathcal{F},\mu,d) vara ett metriskt måttrum vars mått är Borel och 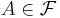A \in \mathcal{F}. Beteckna

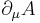\partial_\mu A := \{x \in X : \exist\Theta_\mu (A,x) = \Theta_\mu (X\setminus A,x) = 1 \} .

Då \partial_\mu A, kallas måtteoretiska randen, som är en mängd vars element är tätpunkterna till A och A:s komplement.

Egenskaper

Måtteoretiska randen är en mätbar mängd, men inte nödvändigtvis en rand för A. Till exempel, om

(X,\mathcal{F},\mu,d) = (\R,\mbox{Bor}\,\R,\mathcal{L}_1,|\cdot-\cdot|)

så är randen

\partial \Q = \R.\,

Å andra sidan är måtteoretiska randen

\partial_{\mathcal{L}_1} \Q = \varnothing,

eftersom

\Theta_{\mathcal{L}_1} (\Q,x) = 0 \neq 1 = \Theta_{\mathcal{L}_1} (\R\setminus\Q,x)

för alla x \in \R.

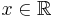Den måtteoretiska randen beror på måttet. Till exempel om måttet 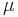\mu \, är räknemåttet så är

\partial_\mu \Q = \R = \partial \Q.

Se även

Referenser

  • Kaimanovich, V. "Measure-theoretic boundaries of Markov chains, 0-2 laws and entropy", Proc. Harmonic Analysis and Discrete Potential Theory, 1991
Hämtad från "https://sv.rilpedia.org/wiki/M%C3%A5tteoretisk_rand"
Personliga verktyg