Kolmogorovrum
Från Rilpedia
Ett Kolmogorovrum eller T0-rum är inom matematik, specifikt topologi, ett topologiskt rum som uppfyller ett visst separationsaxiom.
Innehåll |
Definition
Låt X vara ett topologiskt rum, då X är ett Kolmogorovrum om för alla par av distinkta punkter x och y i X existerar en öppen mängd som innehåller exakt en av punkterna (punkterna är topologiskt urskijbara).
I allmänhet gäller för två punkter x och y i topologiska rum att:
- x och y är separerade
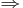 x och y är urskiljbara
x och y är urskiljbara 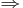 x och y är distinkta.
x och y är distinkta.
I ett Kolmogorovrum är sista pilen en ekvivalenspil, två punkter är distinkta om och endast om de är urskiljbara.
Exempel
Rum som inte är T0
- En mängd med mer än ett element med den triviala topologin, då inga punkter är urskijlbara.
- R2 med öppna mängder som är kartesiska produkter mellan öppna mängder i R och hela R, då punkterna (a,b) och (a,c) är oskiljbara.
Rum som är T0 men inte T1
Zariskitopologin på spektrumet för en kommutativ ring är alltid T0 men i regel inte T1. I ett T1-rum gäller att varje mängd bestående av en punkt är sluten, i ovan nämnda rum kan det finnas primideal som inte är maximala, vilka inte är slutna i Zariskitopologin.
Referenser
- Hocking, John G.; Gail S. Young: Topology, Dover Publications, 1961. ISBN 0-486-65676-4.
- Denna artikel är helt eller delvis baserad på material från engelskspråkiga Wikipedia



