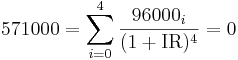Internräntemetoden
Från Rilpedia
Internräntemetoden är en metod för investeringskalkylering. Metoden går ut på att beräkna internräntan, den räntesats som investeringen avkastar. Genom att jämföra internräntan med kalkylräntan, det vill säga uppsatta avkastningskrav, kan investeringens lönsamhet avgöras.
Innehåll |
Översikt
Internräntemetoden ger ett lättbegripligt resultat, som går att jämföra direkt med kalkylräntan för lönsamhetsbedömningar. Resultatet är dessutom möjligt att jämföra för investeringar med olika lång ekonomisk livslängd. Nackdelarna är att den är ganska svår att beräkna, den lämpar sig inte alltför väl för jämförande analys, samt att det kan finnas flera internräntor till samma investering (se Problem med internräntemetoden nedan).
Beräkningar
Beräkningarna av internräntan är nära kopplade till nuvärdemetoden. Den är definierad som den räntesats där en beräkning av nettonuvärdet, det vill säga nuvärde minus grundinvestering, är noll. I följande ekvation är IR internräntan, övriga beteckningar följer sidorna Nuvärdemetoden och Investeringskalkylering.
Tyvärr finns det ingen bra metod för att lösa ut IR direkt, inte ens vid konstanta betalningsöverskott. Vid ett eller två år går det att lösa med förstagradsekvationer och andragradsekvationer. Annars måste numeriska metoder användas. Det bästa sättet är att låta en dator eller miniräknare utföra jobbet. Kalkylprogram har dessutom ofta en inbyggd funktion för att hitta internräntan. Givetvis går det även att lösa det grafiskt, som på bilden till höger.
Beslutsgrunder
- Om internräntan är högre än kalkylräntan är investeringen lönsam.
- Vid jämförelser är det alternativ som har högst internränta som regel mest ekonomiskt fördelaktig.
Problem med internräntemetoden
Skiljer inte på inlåning och utlåning
Jämför följande två projekt:
-
År 0 År 1 År 2 IR NNV (p = 8%) A -100.000 60.000 60.000 13,07% 6.478 B 100.000 -60.000 -60.000 13,07% -6.478
Förlusten i projekt B avspeglas inte i internräntan. Även nuvärdet, eller någon annan metod, måste alltså beräknas. Den här typen av förluster kan vara betydligt svårare att upptäcka än i exemplet ovan.
Orimligt höga räntesatser
Ett stort problem med internräntemetoden är att den utgår ifrån att alla inbetalningar kan återinvesteras till internräntan. Det är naturligtvis inte rimligt, vissa investeringar kan ge internräntor över 50%, vilket inte kommer att avspegla utfallet.
Jämförelser stirrar sig blinda på en punkt
Det är tveksamt om internräntemetoden är bra för jämförelser mellan olika alternativ.
-
Två alternativa investeringar jämförs Betalningsströmmar Nettonuvärden vid olika kalkylräntor 

Exempel 1: Alternativ med restvärde (blått) jämförs med alternativ utan restvärde (grönt).
Om de två alternativen i exempel 1 jämförs, har det gröna alternativet högre internränta (12,75%) än det blå (10%). Ändå är det blå alternativet bättre om kalkylräntan är lägre än 5,35%.
Flera lösningar
Ett annat problem är att det kan finnas flera lösningar för vissa investeringar.
-
Två lösningar till samma investeringsalternativ Betalningsströmmar Nettonuvärden vid olika kalkylräntor 

Exempel 2: Nettonuvärdet är noll vid kalkylräntorna -26,03% och +19,73%.
Villkoret att NNV = 0 uppfylls vid både IR = -26,03% och IR = 19,73%.
Kan sakna lösningar
Det maximala nettonuvärdet i exempel 2 infaller vid kalkylräntan -13%. Värdet är då 35,69. Detta innebär att om grundinvesteringen hade varit 50% större, hade kurvan aldrig korsat x-axeln, och internräntan hade saknat värden!
Jämförelser kan bli oerhört komplexa
Sammantaget kan det ge komplexa jämförelser.
-
Multipla lösningar på två alternativ Betalningsströmmar Nettonuvärden vid olika kalkylräntor 
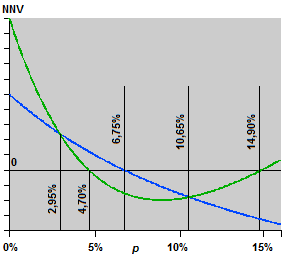
Exempel 3: Jämförelse mellan investeringsalternativ med 4,70% och 14,90% resp. 6,75% internränta.
Se även
Referenser
Tryckta källor
- Brealey, Richard A.; Stewart C. Myers: Principles of corporate finance, McGraw-Hill Companies, Inc., [1981] 1996, fifth ed. (engelska). ISBN 0-07-114053-0.
- Andersson, Göran: Kalkyler som beslutsunderlag, Studentlitteratur, Lund [1983] 2001, 5:e uppl. (svenska). ISBN 91-44-01910-6.
Webbreferenser
- [|Avdelningen Bygg- och Fastighetsekonomi, Institutionen för Fastigheter och Byggande, KTH] (2007). ”Investeringsanalys” (på sv) (PDF). KTH. http://www.infra.kth.se/BYFA/utbildning/grundutbildning/kurser/Ekonomi_AI1103/investeringsanalys_071105.pdf. Läst 3 juni 2008.