Gram-Schmidts ortogonaliseringsprocess
Från Rilpedia
Gram-Schmidts ortogonaliseringsprocess är en algoritm för att generera en ortonormerad (ortogonal och normerad) bas ur en given mängd vektorer tillhörande ett inre produktrum med en skalärprodukt 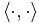 .
.
Metoden är uppkallad efter Erhard Schmidt och Jørgen Pedersen Gram, men dök upp tidigare i verk av Laplace och Cauchy. Iwasawafaktorisering är en generalisering av metoden.
Algoritmen
Steg 0: Ta bort vektorer som gör att givna mängden är linjärt oberoende ur den givna mängden. Antag att denna eventuellt ändrade mängd vektorer är 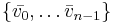 och låt
och låt 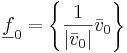 .
.
Steg i (i = 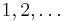 ): Antag att en bas
): Antag att en bas 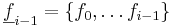 har konstruerats genom att ha använt vektorerna
har konstruerats genom att ha använt vektorerna 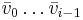 . Om i = n så är algoritmen färdig. Låt
. Om i = n så är algoritmen färdig. Låt 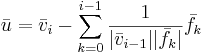 och sätt
och sätt 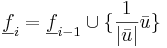 .
.
Här har 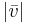 använts för att beteckna
använts för att beteckna 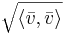 .
.
Algoritmen ger som resultat den ortonormerade mängden 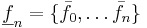 . Att algoritmen vid steg i, i > 0 kräver en linjärt oberoende mängd vektorer inses vid steget
. Att algoritmen vid steg i, i > 0 kräver en linjärt oberoende mängd vektorer inses vid steget 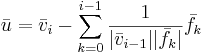 . Om
. Om 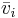 här är linjärt beroende med
här är linjärt beroende med 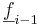 , så är
, så är 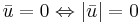 , och uttrycket
, och uttrycket 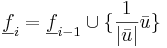 saknar mening.
saknar mening.



