Exakt differentialform
Från Rilpedia
En differentialform 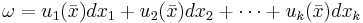 av klass
av klass 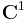 , definierad i ett öppet område
, definierad i ett öppet område 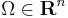 , säges vara exakt om den är differentialen till ett skalärfält, d.v.s. om det finns ett skalärfält Φ i Ω sådant att
, säges vara exakt om den är differentialen till ett skalärfält, d.v.s. om det finns ett skalärfält Φ i Ω sådant att
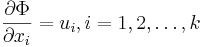
För en differentialform η på en allmän differentierbar mångfald gäller att η är exakt om det finns en form ω sådan att dω = η. Här betecknar d den yttre derivatan.
Varje exakt differentialform av klass 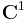 är sluten.
är sluten.



