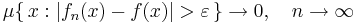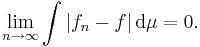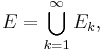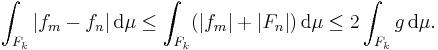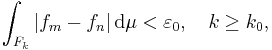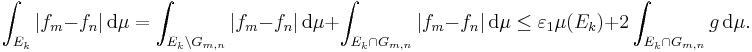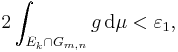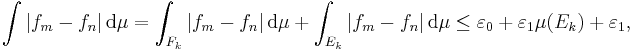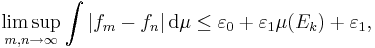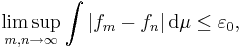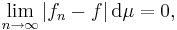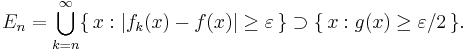Dominerade konvergenssatsen
Från Rilpedia
Dominerade konvergenssatsen förkunnar att om μ är ett mått på en mängd X, fn är en följd av funktioner på X som är integrerbara med avseende på μ, sådana att de antingen konvergerar nästan överallt till en funktion f eller
för varje 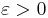 , och
, och 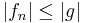 , där g är en integrerbar funktion, så är f integrerbar och
, där g är en integrerbar funktion, så är f integrerbar och
Bevis
Satsen kan bevisas enligt följande. Antag först att
för varje 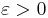 . Låt
. Låt 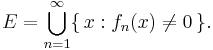 Då är E en σ-ändlig mängd, vilket är uppenbart om μ är ett σ-ändligt mått och eljest är en direkt följd av att fn är integrerbara funktioner. Sålunda kan E skrivas som en union
Då är E en σ-ändlig mängd, vilket är uppenbart om μ är ett σ-ändligt mått och eljest är en direkt följd av att fn är integrerbara funktioner. Sålunda kan E skrivas som en union
där 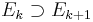 och
och 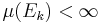 .
.
Låt 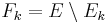 . Då är
. Då är
Det följer att det för varje 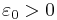 finns ett tal k0 sådant att
finns ett tal k0 sådant att
gäller för varje m och n, alldenstund 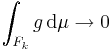 , när
, när 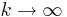 .
.
Låt 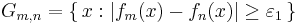 . Då är
. Då är
Ur antagandet om funktionerna fn följer att 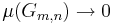 när
när 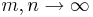 . Sålunda finns ett tal n0 sådant att
. Sålunda finns ett tal n0 sådant att
gäller för varje 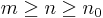 . Detta ger nu att
. Detta ger nu att
om 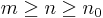 och
och 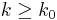 . Härav följer att
. Härav följer att
och sålunda gäller att
eftersom μ(Ek) < 0. Det är nu lätt att se att
vilket bevisar satsen.
För att visa satsen när fn konvergerar till f nästan överallt, räcker det att visa att
för varje 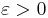 . Låt
. Låt
Eftersom g är integrerbar så är 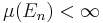 och eftersom
och eftersom 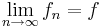 nästan överallt så är
nästan överallt så är 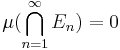 . Det följer att
. Det följer att 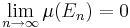 . Enär
. Enär 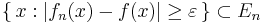 , så följer det att
, så följer det att
för varje 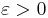 . Detta slutför beviset av satsen.
. Detta slutför beviset av satsen.