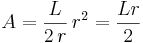Cirkelsektor
Från Rilpedia
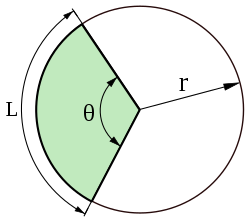
En cirkelsektor (kallas även tårtbit på grund av dess form) är en indelning av en cirkel begränsad av två räta linjer från mittpunkten samt cirkelns periferi. En sträcka ifrån cirkelns mittpunkt ut till periferin kallas radie och krökta linjen längs periferin kallas cirkelbåge.
Arean av en cirkelsektor beräknas genom:
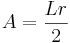
Där L är båglängden (längden på cirkelbågen) och r är radien.
Härledning av formeln för arean
Vi vet att en cirkels totala area beräknas enligt:
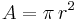
I så fall kan vi tänka oss att desto större sektorns vinkel är, desto större är sektorns area. Då vinkeln är som minst (0 grader/radianer) är även arean som minst (0 a.e.), och då vinkeln är som störst (360 grader/2π radianer), är även arean som störst (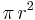 ). Cirkelsektorns area stiger linjärt, då vinkeln blir större.
). Cirkelsektorns area stiger linjärt, då vinkeln blir större.
Härifrån kan vi dra slutsatsen att cirkelsektorns area kan skrivas som cirkelns totala area gånger vinkelns andel av en full vinkel (360 grader/2π radianer). Det vill säga:
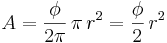
Där φ är cirkelsektorns vinkel uttryckt i radianer.
Då dessutom en vinkels storlek i radianer beräknas enligt
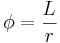
där L är båglängden, och r cirkelns radie, så får vi: