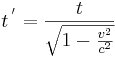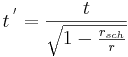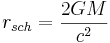Tidsdilatation
Från Rilpedia
Tidsdilatation (tidsutvidgning) beroende på hastighet innebär att om två referenssystem r och r', har identiska klockor, kommer en observatör i r att anse att klockan i r' går långsammare om referenssystemen r och r' befinner sig i relativ rörelse. En observatör i r' anser likaså att klockan i r går långsammare än den lokala klockan. Vid "ordinära" hastigheter kan denna tidsskillnad anses försumbar. Det är först vid hastigheter som är minst 1/10 av ljusets hastighet som den får praktisk betydelse. I den speciella relativitetsteorin behandlas fallet då referenssystemen befinner sig i likformig relativ rörelse.
Enligt den allmänna relativitetsteorin uppstår tidsdilatation med avseende på två punkter i ett gravitationsfält där de två punkterna har olika gravitationell fältstyrka. En klocka går långsammare i den punkt som har den största gravitationella fältstyrkan. En praktisk konsekvens av detta är att GPS-satelliternas atomklockor måste korrigeras med hänsyn till att gravitationen är svagare på satellitbanornas avstånd jämfört med gravitationen vid jordytan.
I svensk text används ofta felaktigt termen tidsdilation, vilket förefaller vara en sammanblandning med engelskan.
Tidsdilatation beroende på hastighet
En ”fotonklocka” skulle kunna konstrueras genom att man låter en foton reflekteras mellan två parallella speglar:
En stationär observatör P ser fotonens bana som fixerad i rummet. En observatör P' i likformig relativ rörelse med hastigheten 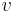 med riktningen parallell med speglarna ser i stället banan som en sekvens av diagonala linjer. P mäter avståndet mellan speglarna till
med riktningen parallell med speglarna ser i stället banan som en sekvens av diagonala linjer. P mäter avståndet mellan speglarna till 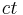 , motsvarande ett ”tick” för klockan. P' mäter samma avstånd till
, motsvarande ett ”tick” för klockan. P' mäter samma avstånd till 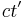 . Då gäller:
. Då gäller:
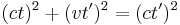 (Pythagoras sats)
(Pythagoras sats)
eller
där 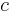 är ljusets hastighet. Man ser att
är ljusets hastighet. Man ser att 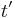 är större än
är större än 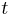 om
om 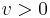 , det vill säga P' tycker att händelseförloppet tar längre tid än vad P gör. Ett grundläggande skäl för den uppmätta tidsskillnaden är att båda observatörerna är överens om ljusets hastighet, vilket mäts till samma värde i alla referenssystem i likformig relativ rörelse. Postulatet om ekvivalens mellan referenssystemen leder då till att tidsparametern måste vara variabel.
, det vill säga P' tycker att händelseförloppet tar längre tid än vad P gör. Ett grundläggande skäl för den uppmätta tidsskillnaden är att båda observatörerna är överens om ljusets hastighet, vilket mäts till samma värde i alla referenssystem i likformig relativ rörelse. Postulatet om ekvivalens mellan referenssystemen leder då till att tidsparametern måste vara variabel.
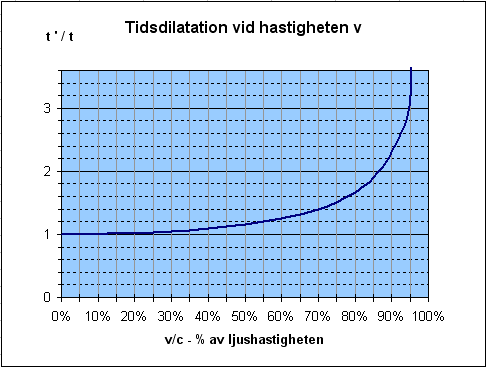
Ju hastigare P' rör sig i förhållande till P, desto långsammare kommer P' att anse att händelsen sker hos P. I extremfallet då hastigheten närmar sig ljusets, kommer tidskillnaden att gå mot oändligheten.
Tidsdilatationen är symmetrisk och lika för båda observatörerna. Om båda observatörerna gör samma experiment, kommer båda att anse att motsvarande händelse hos den andra observatören tar längre tid än den egna lokala händelsen.
Denna symmetriska tillämpning av tidsdilatationen och att alla referenssystem i likformig relativ rörelse postulerades som likvärdiga (samma fysikaliska lagar gäller i samtliga), var det nya i den speciella relativitetsteorin. Hendrik Lorentz, som först formulerade tidsdilatationen (Lorentztransformationerna), föreställde sig att tidsdilatationen bara inträffade för föremål som rörde sig i förhållande till en stillastående eter som antogs uppfylla universum.
Tidsdilatation beroende på gravitation
Antag att en person P som befinner sig på avståndet r från en himlakropp. P gör en mätning av ett händelseförlopp på samma sätt som tidigare och kommer fram till tiden t. En annan person P' som befinner sig på stort avstånd från samma himlakropp och mäter tiden för händelsen hos P kommer då att få tiden t ':
där rsch är den s.k. Schwarzschild-radien för himlakroppen, benämnd efter den tyske astronomen Karl Schwarzschild. Schwarzschild-radien är den radie som en himlakropp skulle behöva krympas till för att bilda ett svart hål. För jorden är denna radie ca 9 mm och för solen ungefär 3 km. För ett svart hål motsvarar denna radie händelsehorisonten, innanför vilken ingenting, vare sig ljus eller materia, kan slippa ut. Av ovanstående formel kan man se, att när P närmar sig Schwarzschildradien så tycks händelser hos P inträffa allt långsammare för avlägsna observatörer. En kropp som faller in mot ett svart hål når i den avlägsne observatörens referenssystem aldrig fram till Schwarzschild-radien (i ett lokalt referenssystem för P där till exempel P befinner sig i vila kommer P att både nå och passera Schwarzschild-radien).
Schwarzschild-radien beror på himlakroppens massa enligt formeln:
där G är gravitationskonstanten och M är kroppens massa.