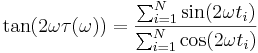Lombs periodogram

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Lombs periodogram är en metod för att skatta frekvensspektrum för data som inte är samplade med jämnt intervall.

Metoden går till enligt följande. Antag att data är xi, tillgängliga vid tidpunkter ti.

Bilda skattningar av medelvärde och varians

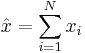
\hat{x}=\sum_{i=1}^{N}{x_i}

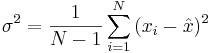
\sigma^2=\frac{1}{N-1}\sum_{i=1}^{N}{(x_i-\hat{x})^2}

Skatta spektrum som funktion av frekvens ω med

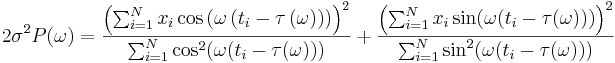
2\sigma^2P(\omega)=\frac{\left(\sum_{i=1}^{N}{x_i\cos\left(\omega\left(t_i-\tau\left(\omega\right)\right)\right)}\right)^2}{\sum_{i=1}^{N}{\cos^2(\omega(t_i-\tau(\omega)))}}+ \frac{\left(\sum_{i=1}^{N}{x_i\sin(\omega(t_i-\tau(\omega)))}\right)^2}{\sum_{i=1}^{N}{\sin^2(\omega(t_i-\tau(\omega)))}}

där

\tan(2\omega\tau(\omega))=\frac{\sum_{i=1}^{N}{\sin(2\omega t_i)}}{\sum_{i=1}^{N}{\cos(2\omega t_i)}}

Hämtad från "https://sv.rilpedia.org/wiki/Lombs_periodogram"
Personliga verktyg