Linjärt ekvationssystem
Från Rilpedia
Ett linjärt ekvationssystem är en uppsättning av ett ändligt antal linjära ekvationer med den algebraiska formen
- a1x + b1y = c1
- a2x + b2y = c2
där an, bn och cn är reella eller komplexa tal. Mer generellt kan ett ekvationssytem med m ekvationer och n obekanta skrivas som
- a11x1 + a12x2 + … + a1nxn = b1
- a21x1 + a22x2 + … + a2nxn = b2
- :
- :
- am1x1 + am2x2 + … + amnxn = bm
Ett sådant ekvationssystem sägs ha en lösning om alla variabler samtidigt uppfyller samtliga ekvationer. Linjära ekvationsystem har antingen ingen lösning, exakt en lösning eller oändligt många lösningar. Om man låter 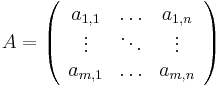 ,
, 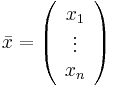 och
och 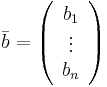 så kan ovanstående ekvationssystem skrivas
så kan ovanstående ekvationssystem skrivas 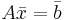 . En sådan ekvation har lösningen
. En sådan ekvation har lösningen 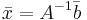 , förutsatt att
, förutsatt att 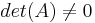 och m = n < math > .Om < math > det(A) = 0 så kan ekvationen endera ha oändligt många lösningar (med ett ändligt antal frihetsgrader) eller ingen lösning. Om m > n så är systemet underbestämt och om m < n så är systemet överbestämt. Det bör noteras att inversen av en icke-kvadratisk matris ej är definierad.
och m = n < math > .Om < math > det(A) = 0 så kan ekvationen endera ha oändligt många lösningar (med ett ändligt antal frihetsgrader) eller ingen lösning. Om m > n så är systemet underbestämt och om m < n så är systemet överbestämt. Det bör noteras att inversen av en icke-kvadratisk matris ej är definierad.
| Exempel på linjära ekvationssystem | |
| x + 5y = 8 | x1 + 2x2 - 3x3 = 14 |
| s = ½x + 3t – 1 | |
| Exempel på ickelinjära ekvationssystem | |
| x + y2 = 0 | |
| s − sint = 0 | 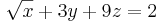 |



