Gränspunkt
Från Rilpedia
För gränspunkter av fastigheter, se gränspunkt (fastighet).
Inom topologi finns det många olika sorters distinktioner av begreppet gränspunkt.
Låt 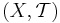 vara ett icke-tomt topologiskt rum.
vara ett icke-tomt topologiskt rum.
En punkt 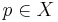 är en gränspunkt till en mängd
är en gränspunkt till en mängd 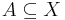 om varje öppen mängd
om varje öppen mängd 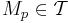 som innehåller punkten, också har minst en punkt,
som innehåller punkten, också har minst en punkt, 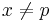 , gemensam med mängden A.
, gemensam med mängden A.
- En gränspunkt
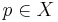 till en mängd A är en omega-ackumuleringspunkt till mängden A om varje öppen mängd
till en mängd A är en omega-ackumuleringspunkt till mängden A om varje öppen mängd 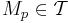 som innehåller punkten p, också har ett uppräkneligt oändligt antal punkter gemensamma med mängden A.
som innehåller punkten p, också har ett uppräkneligt oändligt antal punkter gemensamma med mängden A. - En gränspunkt
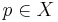 till en mängd A är en kondensationspunkt till mängden A om varje öppen mängd
till en mängd A är en kondensationspunkt till mängden A om varje öppen mängd 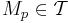 som innehåller punkten p, också har ett överuppräkneligt oändligt antal punkter gemensamma med mängden A.
som innehåller punkten p, också har ett överuppräkneligt oändligt antal punkter gemensamma med mängden A.
En punkt 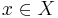 är en gränspunkt till en följd
är en gränspunkt till en följd 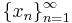 av termer
av termer 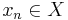 om varje öppen mängd
om varje öppen mängd 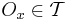 som innehåller punkten x, också innehåller nästan alla termer i följden, med undantag av ändligt många.
som innehåller punkten x, också innehåller nästan alla termer i följden, med undantag av ändligt många.
- En punkt
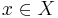 är en ackumuleringspunkt till en följd
är en ackumuleringspunkt till en följd 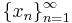 av termer
av termer 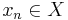 om varje öppen mängd
om varje öppen mängd 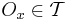 som innehåller punkten x, också innehåller ett uppräkneligt oändligt antal termer ur följden.
som innehåller punkten x, också innehåller ett uppräkneligt oändligt antal termer ur följden.



