Från Rilpedia

Den här artikeln anses undermålig och kan behöva skrivas om helt för att leva upp till Wikipedias artikelstandard. Diskutera frågan på diskussionssidan och förbättra gärna artikeln. Var uppmärksam på artikelns innehåll.

En öppen mängd är ett topologiskt begrepp inom matematik. Man kan definiera en öppen mängd som att en mängd G är öppen om det för varje element 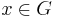finns ett öppet klot kring x som är en delmängd till G.

Öppna mängder är grundläggande i reell och komplex analys och ingår i den mer generella definitionen av kontinuerliga funktioner. De förekommer ofta i samband med metriska rum som i sig är topologiska rum. Topologin definieras där utifrån metriken, och därmed också vilka mängder som är öppna.

Notera

• Öppna mängder är alltid delmängder av ett topologiskt rum.
• Tomma mängden och rummet självt är alltid öppna.
• Tomma mängden och rummet självt är alltid slutna. Detta följer av definitonen av sluten mängd och ovanstående.
• Varje union av öppna mängder är öppen.
• Skärningen av ändligt många öppna mänger är öppen.
• Komplementet till en öppen mängd kallas sluten mängd. Därför är komplementet till en sluten mängd per definition öppen.

En mängd kan vara sluten, öppen, båda öppen och sluten eller ingetdera. För att avgöra vilket som gäller måste man använda definitionen av topologin på rummet.

Exempel

De reella talen är ett metriskt rum och därmed ett topologiskt rum. Där definieras ett öppet intervall (a, b) som 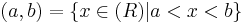En öppen mängd kan sedan definieras som en union av öppna interval.

Denna definition kräver dock två anmärkningar. Dels talar man ofta om öppna bollar (med centrum och radie) i metriska rum snarare är öppna intervall som bara fungerar om man har en ordning (<) som matchar metriken. Dels återstår det att bevisa/konstatera att skärningen mellan två öppna intervall (bollar) i sig kan skrivas som en union av öppna intevall (bollar). Först då kan man säga att ett öppet intervall är en öppen mängd.